Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T08:38:13.416Z Has data issue: false hasContentIssue false
  • English
  • Français

Certain Operators with Rough Singular Kernels

Published online by Cambridge University Press:  20 November 2018

Jiecheng Chen ,
Dashan Fan  and
Yiming Ying
Jiecheng Chen
Affiliation:
Department of Mathematics, Zhejiang University (Xixi Campus), 310028, Hangzhou, China e-mail: [email protected]
Dashan Fan
Affiliation:
Department of Mathematical Science, University of Wisconsin-Milwaukee, Milwaukee, Wisconsin 53201, USA e-mail: [email protected]
Yiming Ying
Affiliation:
Department of Mathematics, Zhejiang University (Xixi Campus), 310028, Hangzhou, China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the singular integral operator

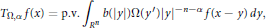$${{T}_{\Omega ,\alpha }}f\left( x \right)\,=\,\text{p}\text{.v}\text{.}\,{{\int }_{{{R}^{n}}}}\,b\left( \left| y \right| \right)\Omega \left( {{y}'} \right){{\left| y \right|}^{-n-\alpha }}\,f\left( x\,-\,y \right)\,dy,$$

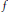defined on all test functions $f$, where $b$ is a bounded function, 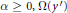$\alpha \ge 0,\,\Omega \left( {{y}'} \right)$ is an integrable function on the unit sphere 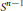${{S}^{n-1}}$ satisfying certain cancellation conditions. We prove that, for 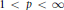$1\,<\,p\,<\infty$, 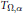${{T}_{\Omega ,\alpha }}$ extends to a bounded operator from the Sobolev space 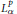$L_{\alpha }^{p}$ to the Lebesgue space 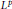${{L}^{p}}$ with 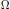$\Omega$ being a distribution in the Hardy space 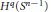${{H}^{q}}\left( {{S}^{n-1}} \right)$ where 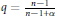$q=\frac{n-1}{n-1+\alpha }$. The result extends some known results on the singular integral operators. As applications, we obtain the boundedness for 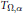${{T}_{\Omega ,\alpha }}$ on the Hardy spaces, as well as the boundedness for the truncated maximal operator 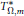$T_{\Omega ,m}^{*}$.

Keywords

42B2042B2542B15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 3 , 01 June 2003 , pp. 504 - 532
Copyright
Copyright © Canadian Mathematical Society 2003

References

[BF] Blank, B. and Fan, D. Hardy spaces on compact Lie groups. Ann. Fac. Sci. Toulouse Math. 6(1997), 429–479.Google Scholar
[BL] Bergh, J. and Lofstrom, J., Interpolation Spaces, An introduction. Grundlehren der MathematischenWissenschafen 233, Spring-Verlag, Berlin, Heidelberg, New York, 1976.Google Scholar
[CDF] Chen, J., Ding, Y. and Fan, D. A class of integral operators with variable kernels in Hardy spaces. Chinese Ann.Math. Ser. A 23(2002), 289–296.Google Scholar
[CF] Chen, J. and Fan, D., Maximal singular integrals on Sobolev spaces. Preprint.Google Scholar
[Ch] Chen, L. On a singular integrals. Studia Math. TLXXXV(1987), 61–72.Google Scholar
[Co1] Colzani, L., Hardy spaces on sphere. Ph.D. Thesis, Washington University, St Louis, Missouri, 1982.Google Scholar
[Co2] Colzani, L. Hardy spaces on Unit Sphere. Boll. Un. Mat. Ital. C (6) Anal. Funz. Appl. IV–C(1985), 219–244.Google Scholar
[CTW] Colzani, L., Taibleson, M. and G.Weiss Maximal estimates for Cesaro and Riesz means on sphere. Indiana Univ.Math. J. (6) 33(1984), 873–889.Google Scholar
[CZ1] Calderon, A. P. and Zygmund, A. On existence of certain singular integrals. Acta. Math. 88(1952), 85–139.Google Scholar
[CZ2] Calderon, A. P. and Zygmund, A. On singular integrals. Amer. J. Math. 18(1956), 289–309.Google Scholar
[CZ3] Calderon, A. P. and Zygmund, A. On singular integrals with variable kernels. Apl. Anal. 7(1978), 221–238.Google Scholar
[DL] Ding, Y. and Lu, S. Homogeneous fractional integrals on Hardy spaces. Tohoku Math. J. 52(2000), 153–162.Google Scholar
[DR] Duoandikoetxea, J. and Rubio, J. L. de Francia Maximal and singular integral operators via Fourier transform estimates. Invent. Math. 84(1986), 541–561.Google Scholar
[Fe] Feferman, R. A note on singular integrals. Proc. Amer.Math. Soc. 74(1979), 266–270.Google Scholar
[FJW] Frazier, M., Jawerth, B. and Weiss, G., Littlewood-Paley Theory and the Study of Function Spaces. AMS-CBMS Regional Conf. Ser.79, Conf. Board Math. Sci., Washington, D.C. Google Scholar
[FP1] Fan, D. and Pan, Y. Singular integral operators with rough kernels supported by subvarieties. Amer. J. Math. 119(1997), 799–839.Google Scholar
[FP2] Fan, D. and Pan, Y. L2 boundedness of a singular integral operators. Publ. Math. 41(1997), 317–333.Google Scholar
[FP3] Fan, D. and Pan, Y. A singular integral operator with rough kernel. Proc. Amer.Math. Soc. 125(1997), 3695–3703.Google Scholar
[GS] Grafakos, L. and Stefanov, , Convolution Calderon-Zygmund singular integral operators with rough kernels. Analysis of divergence Orono, ME, 1997, 119-143, Appl. Numer. Anal., Birkhauser Boston, Massachusetts, 1999.Google Scholar
[HPW] Han, S. Y., Paluszynski, M. and Weiss, G., A new atomic decomposition for the Triebel-Lizorkin spaces. Harmonic Analysis and operator Theory, Caracas, 1994, 235-249, Contemp. Math. 189, Amer. Math. Soc., Providence, Rhode Island, 1995.Google Scholar
[KW] Kurtz, D. and Wheeden, R. L. Results on weighted norm inequalities for multipliers. Trans. Amer. Math. Soc. 255(1979), 343–362.Google Scholar
[MW] Muckenhoupt, B. and Wheeden, R. L. Weighted norm inequalities for singular and fractional integrals. Trans. Amer. Math. Soc. 161(1971), 249–258.Google Scholar
[Na] Namazi, J., A singular integral. Ph. D. Thesis, Indiana University, Bloomington, 1984.Google Scholar
[RW] Ricci, F. and Weiss, G., A characterization of H1(∑n-1). Proc. Sympos. Pure Math. 35, (eds., S. Wainger and G. Weiss), Amer. Math. Soc. Providence, Rhode Island, 289–294.Google Scholar
[S] Sonine, Math. Ann. XXX(1887), 157-161.Google Scholar
[Str] Strichartz, R. S. HP Sobolev spaces. Colloq. Math. LX/LXI(1990), 129–139.Google Scholar
[St] Stein, E. M., Harmonic Analysis: Real-Variable Methods, Orthogonality and Oscillatory Integrals. Princeton University Press, Princeton, New Jersey, 1993.Google Scholar
[SW] Stein, E. M. and Weiss, G., Introduction to Fourier Analysis on Euclidean Spaces. Princeton Univ. Press, Princeton, New Jersey, 1971.Google Scholar
[T] Torres, R., On the boundedness of certain operators with singular kernels on distribution spaces. Mem. Amer. Math. Soc. 442(1992), Amer.Math. Soc.Google Scholar
[Tr] Triebel, H., Interpolation Theory, Function Spaces and Differential Operators, 2nd edition. Johann Ambrosius Barth Verlag, Heidlberg, Leipzig, 1995.Google Scholar