Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:50:29.431Z Has data issue: false hasContentIssue false
  • English
  • Français

Certain Exponential Sums and Random Walks on Elliptic Curves

Published online by Cambridge University Press:  20 November 2018

Tanja Lange  and
Igor E. Shparlinski
Tanja Lange
Affiliation:
Institute for Information Security and Cryptology, Ruhr-University of Bochum, D-44780 Bochum, Germany, e-mail: [email protected]
Igor E. Shparlinski
Affiliation:
Department of Computing, Macquarie University, Sydney, NSW 2109, Australia, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

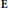For a given elliptic curve $\mathbf{E}$, we obtain an upper bound on the discrepancy of sets of multiples 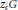${{z}_{s}}G$ where ${{z}_{s}}$ runs through a sequence 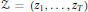$Z\,=\,\left( {{z}_{1}},\ldots ,{{z}_{T}} \right)$ such that 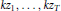$k{{z}_{1}},\ldots ,k{{z}_{T}}$ is a permutation of 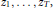${{z}_{1}},\ldots ,{{z}_{T}}$, both sequences taken modulo $t$, for sufficiently many distinct values of $k$ modulo $t$.

We apply this result to studying an analogue of the power generator over an elliptic curve. These results are elliptic curve analogues of those obtained for multiplicative groups of finite fields and residue rings.

Keywords

11L0711T2311T7114H5294A60
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 2 , 01 April 2005 , pp. 338 - 350
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Beelen, P. and Doumen, J., Pseudorandom sequences from elliptic curves. In: Finite Fields with Applications to Coding Theory, Cryptography and Related Areas, Springer-Verlag, Berlin, 2002, pp. 7–52.Google Scholar
[2] Blake, I., Seroussi, G., and Smart, N., Elliptic curves in cryptography. LondonMath. Society Lecture Note Series 265, Cambridge University Press, 2000.Google Scholar
[3] Cusic, T. W., Ding, C., and Renvall, A., Stream ciphers and number theory. North-Holland, Amsterdam, 1998.Google Scholar
[4] El Mahassni, E. and Shparlinski, I. E., On the uniformity of distribution of congruential generators over elliptic curves. In: Sequences and Their Applications, Springer-Verlag, London, 2002, pp. 257–264.Google Scholar
[5] Davenport, H. and Lewis, D. J., Character sums and primitive roots in finite fields. Rend. Circ. Mat. Palermo (2) 12(1963), 129–136.Google Scholar
[6] Friedlander, J. B., Hansen, J., and Shparlinski, I. E., Character sums with exponential functions. Mathematika 47(2000), 75–85.Google Scholar
[7] Friedlander, J. B., Konyagin, S. V., and Shparlinski, I. E., Some doubly exponential sums over Zm. Acta Arith. 105(2002), 349–370.Google Scholar
[8] Friedlander, J. B., Pomerance, C., and Shparlinski, I. E., Period of the power generator and small values of Carmichael's function. Math. Comp. 70(2001), 1591–1605 (see also 71(2002), 1803–1806).Google Scholar
[9] Friedlander, J. B. and Shparlinski, I. E., On the distribution of the power generator. Math. Comp. 70(2001), 1575–1589.Google Scholar
[10] Gong, G., Berson, T. A., and Stinson, D. R., Elliptic curve pseudo random sequence generators. In: Selected Areas in Cryptography, Lecture Notes in Comput. Sci. 1758, Springer-Verlag, Berlin, 2000, pp. 34–49.Google Scholar
[11] Gong, G. and Lam, C. C. Y., Linear recursive sequences over elliptic curves. In: Sequences and Their Applications, Springer, London, 2002, pp. 182–196.Google Scholar
[12] Griffin, F. and Shparlinski, I. E., On the linear complexity profile of the power generator. IEEE Trans. Inform. Theory 46(2000), 2159–2162.Google Scholar
[13] Guajardo, J. and Paar, C., Efficient algorithms for elliptic curve cryptosystems. In: Advances in Cryptology—Crypto’97, Lect. Notes in Comput. Sci. 1294, Springer, Berlin, 1997, pp. 342–356.Google Scholar
[14] Hallgren, S., ‘Linear congruential generators over elliptic curves’, Preprint CS-94-143, Dept. of Comp. Sci., CornegieMellon Univ., 1994, 1–10 Google Scholar
[15] Hess, F. and Shparlinski, I. E., On the linear complexity and multidimensional distribution of congruential generators over elliptic curves. Designs, Codes and Cryptography, (to appear).Google Scholar
[16] Kohel, D. R. and Shparlinski, I. E., Exponential sums and group generators for elliptic curves over finite fields. In: Algorithmic Number Theory, Lecture Notes in Comput. Sci. 1838, Springer, Berlin, 2000, pp. 395–404.Google Scholar
[17] Lagarias, J. C., Pseudorandom number generators in cryptography and number theory. In: Cryptology and Computational Number Theory, Proc. Sympos. Appl. Math. 42, Amer. Math. Soc., Providence, RI, 1990, pp. 115–143.Google Scholar
[18] Lam, C. C. Y. and Gong, G., Randomness of elliptic curve sequences. Research Report CORR 2002-18, Faculty of Mathematics, University of Waterloo,Waterloo, 2002, 1–11 Google Scholar
[19] Lang, S., Elliptic curves: Diophantine analysis. Grundlehren derMathematischenWissenschaften 231, Springer-Verlag, Berlin, 1978.Google Scholar
[20] Lenstra, H. W., Jr., Factoring integers with elliptic curves. Ann of Math. 126(1987), 649–673.Google Scholar
[21] Lidl, R. and Niederreiter, H., Finite fields. Encyclopedia of Mathematics and its Applications, 20, Cambridge University Press, Cambridge, 1997.Google Scholar
[22] Menezes, A. J., van, P. C. Oorschot, and Vanstone, S. A., Handbook of applied cryptography. CRC Press, Boca Raton, FL, 1997.Google Scholar
[23] Schoof, R., Elliptic curves over finite fields and the computation of square roots mod p. Math. Comp. 44(1985), 483–494.Google Scholar
[24] Shparlinski, I. E., On the Naor–Reingold pseudo-random number function from elliptic curves. Appl. Algebra Engrg. Comm. Comput. 11(2000), 27–34.Google Scholar
[25] Shparlinski, I. E., On the linear complexity of the power generator. Des. Codes Cryptogr. 23(2001), 5–10.Google Scholar
[26] Shparlinski, I. E. and Silverman, J. H., On the linear complexity of the Naor–Reingold pseudo-random function from elliptic curves. Des. Codes Cryptogr. 24(2001), 279–289.Google Scholar
[27] Silverman, J. H., The arithmetic of elliptic curves, Springer-Verlag, Berlin, 1995.Google Scholar
[28] Winterhof, A., Some estimates for character sums and applications. Des. Codes Cryptogr. 22(2001), 123–131.Google Scholar