Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T01:07:04.074Z Has data issue: false hasContentIssue false
  • English
  • Français

Centres of Rank-Metric Completions

Published online by Cambridge University Press:  20 November 2018

David Handelman
David Handelman*
Affiliation:
University of Ottawa, Ottawa, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we are primarily concerned with the behaviour of the centre with respect to the completion process for von Neumann regular rings at the pseudo-metric topology induced by a pseudo-rank function.

Let R be a (von Neumann) regular ring, and N a pseudo-rank function (all terms left undefined here may be found in [6]). Then N induces a pseudo-metric topology on R, and the completion of R at this pseudo-metric, 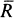, is a right and left self-injective regular ring. Let Z( ) denote the centre of whatever ring is in the brackets. We are interested in the map .

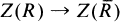If R is simple, Z(R) is a field, so is discrete in the topology; yet Goodearl has constructed an example with Z(R) = R and Z(R) = C [5, 2.10]. There is thus no hope of a general density result.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 6 , 01 December 1985 , pp. 1134 - 1148
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Berberian, S. K., Baer *-rings (Springer-Verlag, Heidelberg/New York, 1972).CrossRefGoogle Scholar
2. Blackadar, B. and Handelman, D., Dimension functions and traces on C*-algebras, J. of Functional Analysis 45 (1982), 297–340.Google Scholar
3. Effros, E. G., Handelman, D. E. and Shen, C.-L., Dimension groups and their affine representations, Amer. J. Math. 102 (1980), 385–407.Google Scholar
4. Farkas, D. and Snider, R., Locally finite dimensional algebras, Proc. Amer. Math. Soc. 81 (1981), 369–372.Google Scholar
5. Goodearl, K. R., Centers of completions of regular rings, Pacific J. Math. 76 (1978), 381–395.Google Scholar
6. Goodearl, K. R., von Neumann regular rings (Pitman, London, 1979).Google Scholar
7. Halperin, I., von Neumann's arithmetics of continuous rings, Acta sci. Math. 23 (1962), 1–17.Google Scholar
8. Halperin, I., Elementary divisors in von Neumann rings, Can. J. Math. 14 (1962), 39–44.Google Scholar
9. Menai, P., On tensor products of algebras being von Neumann regular or selfinjective, Comm. in Algebra 9 (1981), 691–7.Google Scholar
10. Menai, P. and Raphael, R., On epimorphism-final rings, preprint.Google Scholar
11. Renault, G., Algèbre non-commutative (Gauthier-Villars).Google Scholar