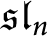 $\mathfrak {sl}_n$
$\mathfrak {sl}_n$Published online by Cambridge University Press: 19 May 2020
Bernstein, Frenkel, and Khovanov have constructed a categorification of tensor products of the standard representation of
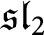 $\mathfrak {sl}_2$
, where they use singular blocks of category
$\mathfrak {sl}_2$
, where they use singular blocks of category
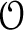 $\mathcal {O}$
for
$\mathcal {O}$
for
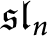 $\mathfrak {sl}_n$
and translation functors. Here we construct a positive characteristic analogue using blocks of representations of
$\mathfrak {sl}_n$
and translation functors. Here we construct a positive characteristic analogue using blocks of representations of
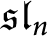 $\mathfrak {s}\mathfrak {l}_n$
over a field
$\mathfrak {s}\mathfrak {l}_n$
over a field
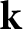 $\mathbf {k}$
of characteristic p with zero Frobenius character, and singular Harish-Chandra character. We show that the aforementioned categorification admits a Koszul graded lift, which is equivalent to a geometric categorification constructed by Cautis, Kamnitzer, and Licata using coherent sheaves on cotangent bundles to Grassmanians. In particular, the latter admits an abelian refinement. With respect to this abelian refinement, the stratified Mukai flop induces a perverse equivalence on the derived categories for complementary Grassmanians. This is part of a larger project to give a combinatorial approach to Lusztig’s conjectures for representations of Lie algebras in positive characteristic.
$\mathbf {k}$
of characteristic p with zero Frobenius character, and singular Harish-Chandra character. We show that the aforementioned categorification admits a Koszul graded lift, which is equivalent to a geometric categorification constructed by Cautis, Kamnitzer, and Licata using coherent sheaves on cotangent bundles to Grassmanians. In particular, the latter admits an abelian refinement. With respect to this abelian refinement, the stratified Mukai flop induces a perverse equivalence on the derived categories for complementary Grassmanians. This is part of a larger project to give a combinatorial approach to Lusztig’s conjectures for representations of Lie algebras in positive characteristic.
Dedicated to our friend, Dmitry Vaintrob
Please note an has been issued for this article.