Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T00:59:22.883Z Has data issue: false hasContentIssue false
  • English
  • Français

A Casselman–Shalika Formula for the Shalika Model of GLn

Published online by Cambridge University Press:  20 November 2018

Yiannis Sakellaridis
Yiannis Sakellaridis*
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA 94305-2125, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Casselman–Shalika method is a way to compute explicit formulas for periods of irreducible unramified representations of 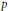$p$-adic groups that are associated to unique models (i.e., multiplicity-free induced representations). We apply this method to the case of the Shalika model of 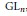$\text{G}{{\text{L}}_{n}}$, which is known to distinguish lifts from odd orthogonal groups. In the course of our proof, we further develop a variant of the method, that was introduced by Y.Hironaka, and in effect reduce many such problems to straightforward calculations on the group.

Keywords

22E5011F7011F85Casselman–ShalikaperiodsShalika modelspherical functionsGelfand pairs
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 5 , 01 October 2006 , pp. 1095 - 1120
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Ash, A. and Ginzburg, D., p-adic L-functions for GL(2n). Invent. Math. 116(1994), no. 1-3, 27–73.Google Scholar
[2] Beineke, J., and Bump, D., A summation formula for divisor functions associated to lattices. Forum Math., to appear.Google Scholar
[3] Brion, M., Quelques propriétés des espaces homogènes sphériques. Manuscripta Math. 55(1986), no. 2, 191–198.Google Scholar
[4] Bump, D. and Friedberg, S., The exterior square automorphic L-functions on GL(n). Israel Math. Conf. Proc. 3, Weizmann, Jerusalem, 1990, 47–65.Google Scholar
[5] Bump, D., Friedberg, S., and Ginzburg, D., Whittaker-orthogonal models, functoriality, and the Rankin-Selberg method. Invent. Math. 109(1992), no. 1, 55–96.Google Scholar
[6] Casselman, W., Introduction to the theory of admissible representations of p-adic reductive groups. http://www.math.ubc.ca/_cass/research/p-adic-book.dvi. Google Scholar
[7] Casselman, W., The unramified principal series of p-adic groups. I. The spherical function. Compositio Math. 40(1980), no. 3, 387–406.Google Scholar
[8] Casselman, W. and Shalika, J., The unramified principal series of p-adic groups. II. The Whittaker function. Compositio Math. 41(1980), no. 2, 207–231.Google Scholar
[9] Friedberg, S. and Jacquet, H., Linear periods. J. Reine Angew.Math. 443(1993), 91–139.Google Scholar
[10] Gelbart, S., Piatetski-Shapiro, I., and Rallis, S., Explicit Constructions of Automorphic L-Functions. Lecture Notes in Mathematics 1254, Springer-Verlag, Berlin, 1987.Google Scholar
[11] Ginzburg, D., Rallis, S., and Soudry, D., Generic automorphic forms on SO(2n + 1): functorial lift to GL(2n), endoscopy, and base change. Internat. Math. Res. Notices 2001, no. 14, 729–764.Google Scholar
[12] Hironaka, Y., Spherical functions and local densities on Hermitian forms. J. Math. Soc. Japan 51(1999), no. 3, 553–581.Google Scholar
[13] Jacquet, H. and Rallis, S., Uniqueness of linear periods. Compositio Math. 102(1996), no. 1, 65–123.Google Scholar
[14] Jacquet, H., and Shalika, J., Exterior square L-functions. In: Automorphic Forms, Shimura Varieties, and L-Functions, Vol. II, Perspect. Math. 11, Academic Press, Boston, MA, 1990, 143–226.Google Scholar
[15] Offen, O., Relative spherical functions on p-adic symmetric spaces (three cases). Pacific J. Math. 215(2004), no. 1, 97–149.Google Scholar
[16] Sato, F., Fourier coefficients of Eisenstein series o. GL n, local densities of square matrices and subgroups of finite abelian groups. Comment. Math. Univ. St. Pauli 54(2005), no. 1, 33–48.Google Scholar
[17] Vinberg, È. B., Complexity of actions of reductive groups. (Russian) Funktsional. Anal. i Prilozhen. 20(1986), no. 1, 1–13. 96.Google Scholar