Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T00:57:57.079Z Has data issue: false hasContentIssue false
  • English
  • Français

C*-Algebras over Topological Spaces: Filtrated K-Theory

Published online by Cambridge University Press:  20 November 2018

Ralf Meyer  and
Ryszard Nest
Ralf Meyer
Affiliation:
Mathematisches Institut and Courant Research Centre, Georg-August Universität Göttingen, 37073 Göttingen, Germany email: [email protected]
Ryszard Nest
Affiliation:
Københavns Universitets Institut for Matematiske Fag, 2100 København, Denmark email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

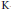We define the filtrated $\text{K}$-theory of a 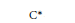${{\text{C}}^{*}}$-algebra over a finite topological space 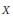$X$ and explain how to construct a spectral sequence that computes the bivariant Kasparov theory over 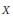$X$ in terms of filtrated 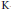$\text{K}$-theory.

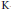For finite spaces with a totally ordered lattice of open subsets, this spectral sequence becomes an exact sequence as in the Universal Coefficient Theorem, with the same consequences for classification.

We also exhibit an example where filtrated $\text{K}$-theory is not yet a complete invariant. We describe two 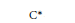${{\text{C}}^{*}}$-algebras over a space 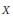$X$ with four points that have isomorphic filtrated 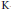$\text{K}$-theory without being 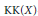$\text{KK}\left( X \right)$-equivalent. For this space 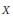$X$, we enrich filtrated 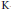$\text{K}$-theory by another 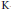$\text{K}$-theory functor to a complete invariant up to 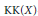$\text{KK}\left( X \right)$-equivalence that satisfies a Universal Coefficient Theorem.

Keywords

19K3546L3546L8046M1846M20
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 2 , 16 April 2012 , pp. 368 - 408
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Beligiannis, A., Relative homological algebra and purity in triangulated categories. J. Algebra 227(2000), no. 1, 268–361. http://dx.doi.org/10.1006/jabr.1999.8237 Google Scholar
[2] Bonkat, A., Bivariante K-Theorie für Kategorien projektiver Systeme von C-Algebren. Ph.D. thesis, Westf. Wilhelms-Universität Münster, 2002. Available at the Deutsche Nationalbibliothek at http://deposit.ddb.de/cgi-bin/dokserv?idn=967387191. Google Scholar
[3] Christensen, J. D., Ideals in triangulated categories: phantoms, ghosts and skeleta. Adv. Math. 136(1998), no. 2, 284–339. http://dx.doi.org/10.1006/aima.1998.1735 Google Scholar
[4] Eilenberg, S. and Moore, J. C., Foundations of relative homological algebra. Mem. Amer. Math. Soc. No. 55 1965.Google Scholar
[5] Kirchberg, E., Das nicht-kommutative Michael-Auswahlprinzip und die Klassifikation nicht-einfacher Algebren. In: C-Algebras. Springer, Berlin, 2000, pp. 92–141.Google Scholar
[6] Meyer, R., Homological algebra in bivariant K-theory and other triangulated categories. II. Tbil. Math. J. 1(2008), 165–210.Google Scholar
[7] Meyer, R. and Nest, R., The Baum–Connes conjecture via localisation of categories. Topology 45(2006), no. 2, 209–259. http://dx.doi.org/10.1016/j.top.2005.07.001 Google Scholar
[8] Meyer, R. and Nest, R., C-Algebras over topological spaces: the bootstrap class. Münster J. Math. 2(2009), 215–252.Google Scholar
[9] Meyer, R. and Nest, R., Homological algebra in bivariant K-theory and other triangulated categories. I. In: Triangulated Categories. London Math. Soc. Lecture Notes 375. Cambridge University Press, Cambridge, 2010, pp. 236–289.Google Scholar
[10] Neeman, A., Triangulated Categories. Annals of Mathematics Studies 148. Princeton University Press, Princeton, NJ, 2001.Google Scholar
[11] Restorff, G., Classification of Cuntz-Krieger algebras up to stable isomorphism. J. Reine Angew. Math. 598(2006), 185–210. http://dx.doi.org/10.1515/CRELLE.2006.074 Google Scholar
[12] Restorff, G., Classification of Non-Simple C-Algebras. Ph.D. thesis, Københavns Universitet, 2008.Google Scholar
[13] Rørdam, M., Classification of extensions of certain C-algebras by their six term exact sequences in K-theory. Math. Ann. 308(1997), no. 1, 93–117. http://dx.doi.org/10.1007/s002080050067 Google Scholar
[14] Vickers, S., Topology via Logic. Cambridge Tracts in Theoretical Computer Science 5. Cambridge University Press, Cambridge, 1989.Google Scholar