Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T00:24:33.459Z Has data issue: false hasContentIssue false
  • English
  • Français

Brauer Groups, Class Groups and Maximal Orders for a Krull Scheme

Published online by Cambridge University Press:  20 November 2018

Heisook Lee  and
Morris Orzech
Heisook Lee
Affiliation:
Ewha Woman's University, Seoul, South Korea
Morris Orzech
Affiliation:
Ewha Woman's University, Seoul, South Korea
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a previous paper [13] one of us considered Brauer groups Br(C) and class groups Cl(C) attached to certain monoidal categories C of divisorial R-lattices. That paper showed that the groups arising for a suitable pair of categories C1 ⊆ C2 could be related by a tidy exact sequence

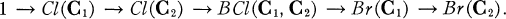
It was shown that this exact sequence specializes to a number of exact sequences which had formerly been handled separately. At the same time the conventional setting of noetherian normal domains was replaced by that of Krull domains, thus generalizing previous results while also simplifying the proofs. This work was carried out in an affine setting, and one aim of the present paper is to carry these results over to Krull schemes. This will enable us to recover the non-affine version of an exact sequence obtained by Auslander [1, p. 261], as well as to introduce a new, non-affine version of a different sequence derived by the same author [2, Theorem 1].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 4 , 01 August 1982 , pp. 996 - 1010
Copyright
Copyright © Canadian Mathematical Society 1982

References

References>

1. Auslander, B., The Brauer group of a ringed space, J. Algebra 4 (1966), 220–273.Google Scholar
2. Auslander, B., Central separable algebras which are locally endomorphism rings of free modules, Proc. Amer. Math. Soc. 80 (1971), 395–404.Google Scholar
3. Auslander, M. and Goldman, O., Maximal orders, Trans. Amer. Math. Soc. 97 (1960), 1–24.Google Scholar
4. Auslander, M. and Goldman, O., The Brauer group of a commutative ring, Trans. Amer. Math. Soc. 97 (1960), 367–409.Google Scholar
5. Bass, H., Algebraic K-theory (W. A. Benjamin, N.Y., 1968).Google Scholar
6. Childs, L. N., Garfinkel, G. and Orzech, M., On the Brauer group and factoriality of normal domains, J. Pure and Applied Algebra 6 (1975), 111–123.Google Scholar
7. DeMeyer, F. and Ingraham, E., Separable algebras over commutative rings Lecture Notes in Mathematics 181 (Springer-Verlag, Berlin, 1971).Google Scholar
8. A., Frôhlich and C. T. C., Wall, Graded monoidal categories, Composito Math. (1974), 229–285.Google Scholar
9. Fossum, R., Maximal orders over Krull domains, J. Algebra 10 (1968), 321–332.Google Scholar
10. Fossum, R., The divisor class group of a Krull domain (Springer-Verlag, New York, 1973).Google Scholar
11. Grothendieck, A., Le groupe de Brauer, II, in Dix exposées sur la cohomologie des schémas (North-Holland, 1968).Google Scholar
12. Hartshorne, R., Algebraic geometry (Springer-Verlag, N.Y., 1977).Google Scholar
13. Orzech, M., Brauer groups and class groups for a Krull domain, in Brauer groups in ring theory and algebraic geometry Lecture Notes in Mathematics 917 (Springer- Verlag, Berlin, 1981).Google Scholar
14. Orzech, M., Divisorial modules and Krull morphisms, J. Pure and Applied Algebra 25 (1982), to appear.Google Scholar
15. Orzech, M. and Small, C., The Brauer group of commutative rings (Marcel Dekker, N.Y., 1975).Google Scholar
16. Pareigis, B., The Brauer group of a monoidal category, in Brauer groups Lecture Notes in Mathematics 549 (Springer-Verlag, Berlin, 1976).Google Scholar
17. Yuan, S., Reflexive modules and algebra class groups over Noetherian integrally closed domains, J. Algebra 32 (1974), 405–417.Google Scholar