Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T01:16:48.096Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounding the Valency of Polygonal Graphs With Odd Girth

Published online by Cambridge University Press:  20 November 2018

Manley Perkel
Manley Perkel*
Affiliation:
Wright State University, Dayton, Ohio
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

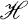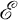In this paper we investigate the action of finite groups G on finite polygonal graphs. The notion of a polygonal graph was introduced in [17]: A polygonal graph is a pair (, ) consisting of a graph 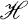which is regular, connected and has girth m for some m ≧ 3, and a set 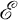of m-gons of 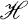such that every 2-claw of 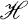is contained in an unique element of 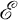(See Section 2 for the définitions of the terms used here.) If 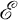is the set of all m-gons of 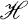, so that there is in 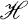an unique m-gon on every one of its 2-claws, then we write 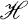for (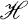, 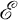) and call 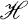a strict polygonal graph. If we wish to emphasize the integer m, then we call (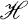, 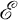) an m-gon-graph (respectively, a strict m-gon-graph).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 6 , 01 December 1979 , pp. 1307 - 1321
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Bender, H., Transitive Gruppen gerader Ordnung, in denenjede Involution genau einen Punkt festldsst, J. Alg. 17 (1971), 527–554.Google Scholar
2. Buekenhout, F., Diagrams for geometries and groups, J. Comb. Th.(A). 27 (1979), 121–151.Google Scholar
3. Buekenhout, F., Doubly transitive groups in which the maximum number of fixed points of involutions is four, Arch. Math. 23 (1972), 362–369.Google Scholar
4. Cameron, P. J., Suborbits in transitive permutation groups, in Combinatorics, Part 3, Mathematical Centre Tracts 57, Amsterdam (1974), 98–129.Google Scholar
5. Coxeter, H. S. M., and Moser, W. O. J., Generators and relations for discrete groups (Ergeb. Math. 14, 3rd edition, Springer, Berlin etc., 1972).Google Scholar
6. Coxeter, H. S. M., Regular poly to pes (3rd edition, Dover, New York, 1973).Google Scholar
7. Dembowski, P., Finite geometries (Ergeb. Math. 44 Springer, Berlin etc., 1968).Google Scholar
8. Gorenstein, D., Finite groups (Harper and Row, New York, Evanston and London, 1968).Google Scholar
9. Gorenstein, D. and Hughes, D. R., Triply transitive groups in which only the identity fixes four letters, 111. J. Math. 5 (1961), 486–491.Google Scholar
10. Hall, M., Jr., The theory of groups (Macmillan, New York, 1959).Google Scholar
11. Harary, F., Graph theory (Addison-Wesley, Reading, 1969).Google Scholar
12. Kantor, W. M., Plane geometries associated with certain 2-transitive groups, J. Alg. 37 (1975), 489–521.Google Scholar
13. Luneburg, H., Uber die Anzahl der Dickson'schen Fastkorper gegebener Ordnung, Atti del Convegno di Geometria Combinatoria e sue Applicazioni, Perugia (1971), 319–322.Google Scholar
14. Manning, H. P., Geometry of four dimensions (1914, Dover, New York, 1958).Google Scholar
15. Perkel, M., A characterization of J\ in terms of its geometry, to appear in Geom. Ded.Google Scholar
16. A characterization of PSL(2, 31) and its geometry, to appear in Can. J. Math.Google Scholar
17. Ph.D. Thesis (University of Michigan, Ann Arbor, Michigan, 1977).Google Scholar
18. Wielandt, H., Finite permutation groups (Academic Press, New York and London, 1964).Google Scholar