Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-20T16:37:11.285Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundary Regularity in the Sobolev Imbedding Theorems

Published online by Cambridge University Press:  20 November 2018

A. E. Hurd
A. E. Hurd*
Affiliation:
University of California, Los Angeles
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In (6) (see also 7), Sobolev introduced a class of function spaces Wm,p(Ω) (m a non-negative integer, 1 < p < ∞) defined on open subsets Ω of Euclidean space En, which have important applications in partial differential equations. They are defined as follows. For each n-tuple α = (α1, … αn) of non-negative integers let

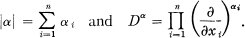
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 18 , 1966 , pp. 350 - 356
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Gagliardo, E., Proprieta di alcune classi difunzioni in più variabilis Ricerche Mat., 7 (1958), 102–137.Google Scholar
2. Kantorovich, L. V., On integral operators, Uspehi Mat. Nauk, 11.2 (68) (1956), 3–29 (Russian).Google Scholar
3. Meyers, N. and Serrin, J., H = W, Proc. Nat. Acad. Sci. U.S.A., 51 (6) (1964), 1055-56.Google Scholar
4. Nirenberg, L., Estimates and existence of solutions of elliptic equations, Comm. Pure Appl. Math., 9 (1956), 509–529.Google Scholar
5. Riesz, M., Sur les ensembles compacts de fonctions sommables, Acta Litt. Ac. Sc. Regiae Univ. Hungaricae F. J. Sectio Sc. Mat. (Szeged), 6 (1932-34), 136–142.Google Scholar
6. Sobolev, S. L., On a theorem of functional analysis, Mat. Sb. 4 (46) (1938), 471–497 (Russian).Google Scholar
7. Sobolev, S. L., Applications of functional analysis in mathematical physics (Providence, 1963).Google Scholar