Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T01:32:30.684Z Has data issue: false hasContentIssue false
  • English
  • Français

The Bott Suspension and the Intrinsic Join

Published online by Cambridge University Press:  20 November 2018

James A. Leise
James A. Leise*
Affiliation:
University of Wisconsin-Milwaukee, Milwaukee, Wisconsin
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If (G ; U, V) is a triad with G a group we define

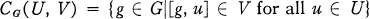
where [g, u] = gug-1u-1 is the commutator. CG(U, V) will be called the (left) center of U in G modulo V or in brief a (left) C-space. If G is a topological group it will be understood that the topology on CG(U, V) is the relative topology of G.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 6 , 01 December 1975 , pp. 1211 - 1221
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Blakers, A. L. and Massey, W. S., Products in homotopy theory, Ann. of Math. 58 (1953), 295–324.Google Scholar
2. Bott, R., A note on the Samelson product in the classical groups, Comment. Math. Helv. 34 (1960), 249–256.Google Scholar
3. Husseini, S. Y., A note on the intrinsic join of Stiefel manifolds, Comment. Math. Helv. 37 (1963), 26–30.Google Scholar
4. James, I. M.. The intrinsic join, Proc. London Math. Soc. 8 (1958), 507–535.Google Scholar
5. James, I. M. Products between homotopy groups, Compositio Math. 23 (1971), 329–345.Google Scholar
6. Lundell, A. T., A Bott map for non-stable homotopy of the unitary group, Topology 8 (1969), 209–217.Google Scholar
7. Lundell, A. T., Torsion in K-theory and the Bott maps (to appear).Google Scholar
8. Whitehead, G. W., On mappings into group-like spaces, Comment. Math. Helv. 28 (1954), 320–329.Google Scholar