Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T01:56:30.282Z Has data issue: false hasContentIssue false
  • English
  • Français

The Bochner–Schoenberg–Eberlein Property and Spectral Synthesis for Certain Banach Algebra Products

Published online by Cambridge University Press:  20 November 2018

Eberhard Kaniuth
Eberhard Kaniuth*
Affiliation:
Institut für Mathematik, Universität Paderborn, D-33095 Paderborn, Germany e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

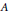Associated with two commutative Banach algebras $A$ and 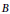$B$ and a character $\theta $ of 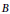$B$ is a certain Banach algebra product 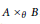$A\,{{\times }_{\theta }}\,B$, which is a splitting extension of 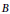$B$ by 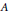$A$. We investigate two topics for the algebra 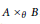$A\,{{\times }_{\theta }}\,B$ in relation to the corresponding ones of 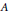$A$ and 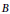$B$. The first one is the Bochner–Schoenberg–Eberlein property and the algebra of Bochner–Schoenberg–Eberlein functions on the spectrum, whereas the second one concerns the wide range of spectral synthesis problems for 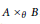$A\,{{\times }_{\theta }}\,B$.

Keywords

46J1046J2543A3043A45commutative Banach algebrasplitting extensionGelfand spectrumset of synthesisweak spectral setmultiplier algebraBSE-algebraBSE-function
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 4 , 01 August 2015 , pp. 827 - 847
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Bade, W. and Curtis, P.C Jr., The Wedderburn decomposition of commutative Banach algebras. Amer. J. Math. 82(1960), 851–866.http://dx.doi.org/10.2307/2372944 Google Scholar
[2] Baggett, L. and Taylor, K., A sufficient condition for the complete reducibility of the regular representation. J. Funct. Anal. 34(1979), 250–265.http://dx.doi.Org/10.1016/0022-1236(79)90033-8 Google Scholar
[3] Bochner, S., A theorem on Fourier-Stieltjes integrals. Bull. Amer. Math. Soc. 40(1934), 271–276.http://dx.doi.org/10.1090/S0002-9904-1934-05843-9 Google Scholar
[4] Cowling, M., The Fourier-Stieltjes algebra of a semisimple group. Colloq. Math. 41(1979), 89–94.Google Scholar
[5] Eberlein, W. F., Characterizations of Fourier-Stieltjes transforms. Duke Math. J. 22(1955), 465–468.http://dx.doi.org/10.1215/S0012-7094-55-02251-1 Google Scholar
[6] Eymard, P., L’algèbre de Fourier d’une groupe localement compact. Bull. Soc. Math. France 92(1964), 181–236.Google Scholar
[7] Figà-Talamanca, A., Positive definite functions which vanish at infinity. Pacific J. Math. 69(1977),355–363.http://dx.doi.org/10.2140/pjm.1977.69.355 Google Scholar
[8] Jones, C. A. and Lahr, C. D., Weak and norm approximate identities are different. Pacific J. Math. 72(1977), 99–104.http://dx.doi.org/10.2140/pjm.1977.72.99 Google Scholar
[9] Inoue, J. and Takahasi, S.-E., On characterizations of the image of the Gelfand transform of commutative Banach algebras. Math. Nachr. 280(2007), 105–126.http://dx.doi.org/10.1002/mana.200410468 Google Scholar
[10] Kamali, Z. and Lashkarizadeh Bami, M., The multiplier algebra and BSE property of the direct sum of Banach algebras. Bull. Austral. Math. Soc. 88(2013), 250–258.http://dx.doi.org/10.1017/S0004972712001001 Google Scholar
[11] Kaniuth, E., Weak spectral synthesis in commutative Banach algebras. J. Funct. Anal. 254(2008), 987–1002.http://dx.doi.Org/10.1016/j.jfa.2007.10.002 Google Scholar
[12] Kaniuth, E., A course in commutative Banach algebras. Graduate Texts in Math. 246, Springer, New York, 2009.Google Scholar
[13] Kaniuth, E., Weak spectral synthesis in commutative Banach algebras. II. J. Funct. Anal. 259(2010),524–544.http://dx.doi.Org/10.1016/j.jfa.2O10.04.011 Google Scholar
[14] Kaniuth, E. and Ülger, A., The Bochner-Schoenberg-Eberlein property for commutative Banach algebras, especially Fourier and Fourier-Stieltjes algebras. Trans. Amer. Math. Soc. 362(2010), 4331–4356. http://dx.doi.org/10.1090/S0002-9947-10-05060-9 Google Scholar
[15] Kaniuth, E., Lau, A. T. and Ülger, A., Homomorphisms of commutative Banach algebras and extensions to multiplier algebras with applications to Fourier algebras. Studia Math. 183(2007), 35–62. http://dx.doi.org/10.4064/sm183-1-3 Google Scholar
[16] Kaniuth, E., Lau, A. T. and Ülger, A., The Rajchman algebra B0(G) of a locally compact group. Submitted.Google Scholar
[17] Larsen, R., An introduction to the theory of multipliers. Springer, New York, 1971.Google Scholar
[18] Lau, A. T., Analysis on a class of Banach algebras with applications to harmonic analysis on locally compact groups and semigroups. Fund. Math. 118(1983), 161–175.Google Scholar
[19] Monfared, M. S., On certain products of Banach algebras with applications to harmonic analysis. Studia Math. 178(2007), 277–294. http://dx.doi.Org/10.4064/sm178-3-4 Google Scholar
[20] Monfared, M. S., Character amenability of Banach algebras. Math. Proc. Camb. Phil. Soc. 144(2008), 697–706.http://dx.doi.org/10.1017/S0305004108001126 Google Scholar
[21] Muraleedharan, M. and Parthasarathy, K., Difference spectrum and spectral synthesis. Tohoku Math. J. 51(1999), 65–73.http://dx.doi.Org/10.2748/tmj/1178224853 Google Scholar
[22] Pier, J.-P., Amenable locally compact groups. Wiley Interscience, New York, 1984.Google Scholar
[23] Rudin, W., Fourier analysis on groups. Interscience, New York, 1962.Google Scholar
[24] Schoenberg, I. J., A remark on the preceding note by Bochner. Bull. Amer. Math. Soc. 40(1934),277–278.http://dx.doi.org/10.1090/S0002-9904-1934-05845-2 Google Scholar
[25] Takahasi, S.-E. and Hatori, O., Commutative Banach algebras which satisfy a Bochner-Schoenberg-Eberlein-type theorem. Proc. Amer. Math. Soc. 110(1990), 149–158.Google Scholar
[26] Takahasi, S.-E. and Hatori, O., Commutative Banach algebras and BSE-inequalities. Math. Japonica 37(1992), 47–52.Google Scholar
[27] Takahasi, S.-E., Takahashi, Y., Hatori, O. and Tanahashi, K., Commutative Banach algebras and BSE-norm. Math. Japonica 46(1997), 273–277.Google Scholar
[28] Ülger, A., Multipliers with closed range on commutative Banach algebras. Studia Math. 153(2002), 59–80.http://dx.doi.org/10.4064/sm153-1-5 Google Scholar
[29] Varopoulos, N. Th., Spectral synthesis on spheres. Math. Proc. Camb. Phil. Soc. 62(1966), 379–387.http://dx.doi.org/10.1017/S0305004100039967 Google Scholar
[30] Warner, C. R., Weak spectral synthesis. Proc. Amer. Math. Soc. 99(1987), 244–248.http://dx.doi.org/10.1090/S0002-9939-1987-0870779-7 Google Scholar