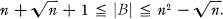Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-25T22:56:12.444Z Has data issue: false hasContentIssue false
  • English
  • Français

Blocking Sets in Projective Spaces

Published online by Cambridge University Press:  20 November 2018

Gary L. Ebert
Gary L. Ebert*
Affiliation:
Texax Tech University, Lubbock, Texas; University of Delaware, Newark, Delaware
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Blocking sets in projective spaces have been of interest for quite some time, having applications to game theory (see [6; 7]) as well as finite nets and partial spreads (see [5]). In [4] Bruen showed that if B is a blocking set in a projective plane of order n, then

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 30 , Issue 4 , 01 August 1978 , pp. 856 - 862
Copyright
Copyright © Canadian Mathematical Society 1978

References

1. Beutelspacher, A., Partial spreads infinite projective spaces and partial designs, Math. Z. 1/5 (1975), 211–229.Google Scholar
2. Bruck, R. H. and Bose, R. C., The construction of translation planes from projective spaces, J. Algebra 1 (1964), 85–102.Google Scholar
3. Bruen, A., Baer subplanes and blocking sets, Bull. Amer. Math. Soc. 76 (1970), 842–344.Google Scholar
4. Bruen, A., Blocking sets infinite projective planes, SIAM J. Appl. Math. 21 (1971), 380–892.Google Scholar
5. Bruen, A., Partial spreads and replaceable nets, Can. j . Math. 23 (1971), 381–891.Google Scholar
6. Hoffman, A. J. and Richardson, M., Block design games, Can. J. Math. 13 (1961), 110–128.Google Scholar
7. Richardson, M., On finite projective games, Proc. Amer. Math. Soc. 7 (1956), 453–465.Google Scholar
8. von Neumann, J. and Morgenstern, O., Theory of games and economic behavior (2nd éd., Princeton Univ. Press, Princeton, 1947).Google Scholar