Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Douglas, Ronald G.
and
Kaminker, Jerome
1997.
Induced Cyclic Cocycles and Higher Eta Invariants.
Journal of Functional Analysis,
Vol. 147,
Issue. 2,
p.
301.
Loday, Jean-Louis
1998.
Cyclic Homology.
Vol. 301,
Issue. ,
p.
257.


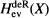 , the even dimensional deRham homology of
, the even dimensional deRham homology of 