Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-13T18:48:40.240Z Has data issue: false hasContentIssue false
  • English
  • Français

Bipositive and Isometric Isomorphisms of Some Convolution Algebras

Published online by Cambridge University Press:  20 November 2018

R. E. Edwards
R. E. Edwards*
Affiliation:
Institute of Advanced Studies, Australian National University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this paper the term "space" will mean "Hausdorff locally compact space" and the term '"group" will mean "Hausdorff locally compact group." If G is a group and 1 ≤ p < ∞, Lp(G) denotes the usual Lebesgue space formed relative to left Haar measure on G. It is well known that L1(G) is an algebra under convolution, and that the same is true of Lp(G) whenever G is compact. We introduce also the space Cc(G) of complex-valued continuous functions f on G for each of which the support (supp f), is compact. The "natural" topology of CC(G) is obtained by regarding CC(G) as the inductive limit of its subspaces

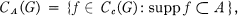
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 17 , 1965 , pp. 839 - 846
Copyright
Copyright © Canadian Mathematical Society 1965

References

1. Dieudonn, J.é et Schwartz, L., La dualité dans les espaces et , Ann. Inst. Fourier Grenoble, 1 (1949), 61–101.Google Scholar
2. Johnson, B. E., Isometric isomorphism of measure algebras, Proc. Amer. Math. Soc, 15 (2) (1964), 186–188.Google Scholar
3. Kawada, Y., On the group ring of a topological group, Math. Japon., 1 (1948), 1–5.Google Scholar
4. Nachbin, L., Topological vector spaces of continuous functions, Proc. Nat. Acad. Sci. U.S.A., 40 (1954), 471–474.Google Scholar
5. Rudin, W., Fourier analysis on groups (New York, 1962).Google Scholar
6. Shirota, T., On locally convex vector spaces of continuous functions, Proc. Japan Acad., 30 (1954), 294–299.Google Scholar
7. Wendel, J. G., On isometric isomorphism of group algebras, Pacific J. Math., 1 (1951), 305–311.Google Scholar
8. Wendel, J. G., Left centralizers and isomorphisms of group algebras, Pacific J. Math., 2 (1952), 251–261.Google Scholar