Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-22T22:52:52.527Z Has data issue: false hasContentIssue false
  • English
  • Français

Best Polynomial Approximation with Linear Constraints

Published online by Cambridge University Press:  20 November 2018

K. Pan  and
E. B. Saff
K. Pan
Affiliation:
Department of Mathematics, University of California, Riverside, California 92521, USA
E. B. Saff
Affiliation:
Institute for Constructive Mathematics, Department of Mathematics, University of South Florida, Tampa, Florida 33620, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a (k + 1) × (k + 1) nonzero matrix. For polynomials p ∈ Pn, set 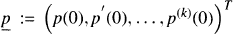and 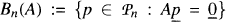. Let E ⊂ C be a compact set that does not separate the plane and f be a function continuous on E and analytic in the interior of E. Set 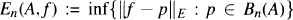and 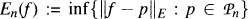. Our goal is to study approximation to f on E by polynomials from Bn(A). We obtain necessary and sufficient conditions on the matrix A for the convergence En(A,f) → 0 to take place. These results depend on whether zero lies inside, on the boundary or outside E and yield generalizations of theorems of Clunie, Hasson and Saff for approximation by polynomials that omit a power of z. Let 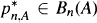be such that 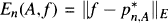. We also study the asymptotic behavior of the zeros of 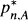and the asymptotic relation between En(f) and En(A,f).

Keywords

41A29
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 44 , Issue 6 , 01 December 1992 , pp. 1289 - 1302
Copyright
Copyright © Canadian Mathematical Society 1992

References

[BSS] Blatt, H.-P., Saff, E.B. and Simkani, M., Jentzsch -Szego type theorems for zeros of best approximatifs, J. London Math. Soc . (2) 38(1980), 307–316.Google Scholar
[CHS] Clunie, J., Hasson, M. and Saff, E.B., Approximation by polynomials that omit a power of z, Approx. Theory & its Appl. 3(1987), 63–73.Google Scholar
[N] Nersesyan, A.A., Uniform approximation with simultaneous interpolation by analytic functions, Izv. Akad. Nauk Armyan. SSR. Mat. 15(1980), 249-257.(in Russian). See also Soviet J. Contemporary Math. Anal. (4) 15(1980), 1–9.Google Scholar
[ST] Saff, E.B. and Totik, V., Behavior of polynomials of best uniform approximation, Trans. Amer. Math. Soc. 316(1988), 567–593.Google Scholar
[T] Tsuji, M., Potential Theory in Modern Function Theory, 2nd éd., Chelsea Publishing Company, New York, NY, (1958).Google Scholar
[W] Walsh, J.L., Interpolation and Approximation by Rational Functions in the Complex Domain, 5th éd., Amer. Math. Soc. Colloquium Publ. 20(1969), Providence, Rhode Island.Google Scholar