Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T01:02:20.516Z Has data issue: false hasContentIssue false
  • English
  • Français

The Bergman Projection on Weighted Norm Spaces

Published online by Cambridge University Press:  20 November 2018

Jacob Burbea
Jacob Burbea*
Affiliation:
University of Pittsburgh, Pittsburgh, Pennsylvania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Quite recently Bekollé and Bonami [1] have characterized the weighted measures λ on the unit disk Δ for which the Bergman projection is bounded on Lp(Δ : λ), 1 < p < ∞. Our methods in [4] can be applied to even extend their result by replacing the unit disk with multiply connected domains. This is done via a rather interesting identity between the Bergman kernel and its “adjoint” [2]. As a corollary of our result we obtain a generalization of a result due to Shikhvatov [7].

Let D be a bounded plane domain and let λ be a positive locally integrate function in D. λ is said to belong to Mp(D) (1 < p < ∞) if it satisfies the Muckenhoupt condition:

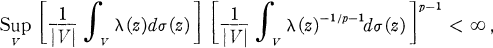
where the supremum is taken over all sectors V ⊂ D, dσ is the area Lebesgue measure and |V| = σ(V).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 4 , April 1980 , pp. 979 - 986
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Bekollé, D. and Bonami, A., Inégalites à poids pour le noyau de Bergman, C. R. Acad. Sc. Paris 286 (1978), 775–778.Google Scholar
2. Bergman, S. and Schiffer, M., Kernel functions and conformai mapping, Compositio Math. 8 (1951), 205–249.Google Scholar
3. Block, I. E., Kernel function and class L2, Proc. Amer. Math. Soc. 4 (1953), 110–117.Google Scholar
4. Burbea, J., Projections on Bergman spaces over plane domains, Can. J. Math. 31 (1979), 1269–1280.Google Scholar
5. Coifman, R. R. and Fefferman, C., Weighted norm inequalities for maximal functions and singular integrals, Studia Math. 51 (1974), 241–250.Google Scholar
6. Pommerenke, Chr., Univalent functions (Vandenhoeck and Ruprecht, Göttingen, 1975).Google Scholar
7. Shikhvatov, A. M., Spaces of analytic functions in a region with an angle, Mat. Zametki 18 (1975), 411–420.Google Scholar