Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T23:07:13.605Z Has data issue: false hasContentIssue false
  • English
  • Français

Beltrami Equation with Coefficient in Sobolev and Besov Spaces

Published online by Cambridge University Press:  20 November 2018

Victor Cruz ,
Joan Mateu  and
Joan Orobitg
Victor Cruz
Affiliation:
Instituto de Física y Matemáticas, Universidad Tecnológica de la Mixteca, 69000 Huajuapan de León, Oaxaca, México, e-mail: [email protected]
Joan Mateu
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193 Bellaterra, Barcelona, Catalonia, e-mail: [email protected]@mat.uab.cat
Joan Orobitg
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193 Bellaterra, Barcelona, Catalonia, e-mail: [email protected]@mat.uab.cat
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

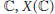Our goal in this work is to present some function spaces on the complex plane $\mathbb{C},\,X(\mathbb{C})$, for which the quasiregular solutions of the Beltrami equation, 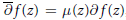$\bar{\partial }f(z)\,=\,\mu (z)\partial f(z)$, have first derivatives locally in 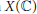$X(\mathbb{C})$, provided that the Beltrami coefficient 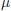$\mu $ belongs to 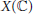$X(\mathbb{C})$.

Keywords

30C6235J9942B20quasiregular mappingsBeltrami equationSobolev spacesCalderón-Zygmund operators
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 6 , 01 December 2013 , pp. 1217 - 1235
Copyright
Copyright © Canadian Mathematical Society 2013

References

[Ah] Ahlfors, L., Lectures on quasiconformal mappings. Second ed., University Lecture Series, 38, American Mathematical Society, Providence, RI, 2006.Google Scholar
[AIM] Astala, K., Iwaniec, T., and Martin, G., Elliptic partial differential equations and quasiconformal mappings in the plane. Princeton Mathematical Series, 48, Princeton University Press, Princeton, NJ, 2009.Google Scholar
[Ba] Bagby, R. J., A characterization of Riesz potentials, and an inversion formula. Indiana Univ. Math. J. 29(1980), no. 4, 581–595. http://dx.doi.org/10.1512/iumj.1980.29.29044 Google Scholar
[BFL] Baratchart, L., Fischer, Y., and Leblond, J., Dirichlet/Neumann problems and Hardy classes for the planar conductivity equation. arxiv:1111.6776v3 Google Scholar
[Br1] Brezis, H., Functional analysis, Sobolev spaces and partial differential equations. Universitext, Springer, New York, 2011.Google Scholar
[Br2] Brezis, H., How to recognize constant functions. A connection with Sobolev spaces. Russian Math. Surveys 57(2002), no. 2, 693–708.Google Scholar
[CFMOZ] Clop, A., Faraco, D., Mateu, J., Orobitg, J., and Zhong, X., Beltrami equations with coefficient in the Sobolev spaceW1;p. Publ. Mat. 53(2009), no. 1, 197–230.Google Scholar
[CFR] Clop, A., Faraco, D., and Ruiz, A., Stability of Calderón's inverse conductivity problem in the plane for discontinuous conductivities. Inverse Probl. Imaging 4(2010), no. 1, 49–91. http://dx.doi.org/10.3934/ipi.2010.4.49 Google Scholar
[CoP] Cobos, F. and Persson, L.-E., Real interpolation of compact operators between quasi-Banach spaces. Math. Scand. 82(1998), no. 1, 138–160.Google Scholar
[CT] Cruz, V. and Tolsa, X., The smoothness of the Beurling transform of characteristic functions of Lipschitz domains. J. Funct. Anal. 262(2012), no. 10, 4423–4457. http://dx.doi.org/10.1016/j.jfa.2012.02.023 Google Scholar
[FTW] Frazier, M., Torres, R., and Weiss, G., The boundedness of Calderón-Zygmund operators on the spaces Fαp;q. Rev. Mat. Iberoamericana 4(1988), no. 1, 41–72. http://dx.doi.org/10.4171/RMI/63 Google Scholar
[Gr] Grafakos, L., Modern Fourier analysis. Second ed., Graduate Texts in Mathematics, 250, Springer, New York, 2009.Google Scholar
[Iw] Iwaniec, T., Lp-theory of quasiregular mappings. In: Quasiconformal space mappings, Lecture Notes in Math., 1508, Springer, Berlin, 1992, pp. 39–64.Google Scholar
[JHL] Jiecheng, C., Houyu, J., and Liya, J., Boundedness of rough oscillatory singular integral on Triebel-Lizorkin spaces. J. Math. Anal. Appl. 306(2005), no. 2, 385–397. http://dx.doi.org/10.1016/j.jmaa.2005.01.015 Google Scholar
[MOV] Mateu, J., Orobitg, J., and Verdera, J., Extra cancellation of even Calderón-Zygmund operators and quasiconformal mappings. J. Math. Pures Appl. 91(2009), no. 4, 402–431.Google Scholar
[Me] Meyer, Y., Continuitó sur les espaces de Hölder et de Sobolev des opérateurs définis par des intégrales singuliàres. In: Recent progress in Fourier analysis (El Escorial, 1983), North-Holland Math. Stud., 111, North-Holland, Amsterdam, 1985, pp. 145–172.Google Scholar
[RS] Runst, T. and Sickel, W., Sobolev spaces of fractional order, Nemytskij operators, and nonlinear partial differential equations. de Gruyter Series in Nonlinear Analysis and Applications, 3, Walter de Gruyter & Co., Berlin, 1996. [Sch] M. Schechter, Principles of functional analysis. Second ed., Graduate Studies in Mathematics, 36, American Mathematical Society, Providence, RI, 2002.Google Scholar
[St] Stein, E. M., Singular integrals and differentiability properties of functions. Princeton Mathematical Series, 30, Princeton University Press, Princeton, NJ, 1970.Google Scholar
[St2] Stein, E. M., Editor's note: the differentiability of functions in Rn. Ann. of Math. (2) 113(1981), no. 2, 383–385.Google Scholar
[Str] Strichartz, R. S., Multipliers on fractional Sobolev spaces. J. Math. Mech. 16(1967), 1031–1060.Google Scholar
[Tri1] Triebel, H., Theory of function spaces. Monographs in Mathematics, 78, BirkhÄuser Verlag, Basel, 1983.Google Scholar
[Tri2] Triebel, H., Sampling numbers and embedding constants. Tr. Mat. Inst. Steklova 248(2005), Issled. po Teor. Funkts. i Differ. Uravn., 275–284; translation in Proc. Steklov Inst. Math. 2005, no. 1 (248), 268–277.Google Scholar
[Tar] Tartar, L., An introduction to Sobolev spaces and interpolation spaces. Lecture Notes of the Unione Matematica Italiana, 3, Springer, Berlin; UMI, Bologna, 2007.Google Scholar
[To] Tolsa, X., Regularity of C1 and Lipschitz domains in terms of the Beurling transform. J. Math. Pures Appl. Available online October 25, 2012. http://dx.doi.org/10.1016/j.matpur.2012.10.014 Google Scholar
[U] Uchiyama, A., On the compactness of operators of Hankel type. Tohoku Math. J. (2) 30(1978), no. 1, 163–171. http://dx.doi.org/10.2748/tmj/1178230105 Google Scholar