Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Altintaş, Osman
Özkan, Öznur
and
Srivastava, H.M.
2001.
Majorization by starlike functions of complex order.
Complex Variables, Theory and Application: An International Journal,
Vol. 46,
Issue. 3,
p.
207.


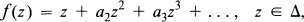
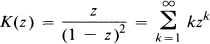
 .
.