Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T04:32:54.735Z Has data issue: false hasContentIssue false
  • English
  • Français

The Batalin–Vilkovisky Algebra in the String Topology of Classifying Spaces

Part of: Fiber spaces and bundles Quantum field theory; related classical field theories Homotopy theory

Published online by Cambridge University Press:  09 January 2019

Katsuhiko Kuribayashi  and
Luc Menichi
Katsuhiko Kuribayashi
Affiliation:
Department of Mathematical Sciences, Faculty of Science, Shinshu University, Nagano 390-8621, Japan Email: [email protected]
Luc Menichi
Affiliation:
LAREMA - UMR CNRS 6093, Université d’Angers, 2 Boulevard Lavoisier, 49045 Angers, France Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For almost any compact connected Lie group 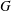$G$ and any field 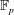$\mathbb{F}_{p}$, we compute the Batalin–Vilkovisky algebra 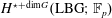$H^{\star +\text{dim}\,G}(\text{LBG};\mathbb{F}_{p})$ on the loop cohomology of the classifying space introduced by Chataur and the second author. In particular, if 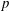$p$ is odd or 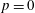$p=0$, this Batalin–Vilkovisky algebra is isomorphic to the Hochschild cohomology 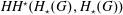$HH^{\star }(H_{\star }(G),H_{\star }(G))$. Over 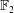$\mathbb{F}_{2}$ , such an isomorphism of Batalin–Vilkovisky algebras does not hold when 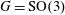$G=\text{SO}(3)$ or 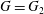$G=G_{2}$. Our elaborate considerations on the signs in string topology of the classifying spaces give rise to a general theorem on graded homological conformal field theory.

Keywords

string topologyBatalin–Vilkovisky algebraclassifying space

MSC classification

Primary: 55P50: String topology
Secondary: 55R35: Classifying spaces of groups and $H$-spaces 81T40: Two-dimensional field theories, conformal field theories, etc.
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 4 , August 2019 , pp. 843 - 889
Copyright
© Canadian Mathematical Society 2018 

Footnotes

The first author was partially supported by JSPS KAKENHI Grant Number 25287008.

References

Behrend, Kai, Ginot, Grégory, Noohi, Behrang, and Xu, Ping, String topology for stacks . Astérisque(2012), no. 343.Google Scholar
Berglund, Alexander and Börjeson, Kaj, Free loop space homology of highly connected manifolds . Forum Math. 29(2017), no. 1, 201–228. https://doi.org/10.1515/forum-2015-0074.Google Scholar
Bredon, Glen E., Sheaf theory . Second ed., Graduate Texts in Mathematics, 170. Springer-Verlag, New York, 1997. https://doi.org/10.1007/978-1-4612-0647-7.Google Scholar
Chas, Moira and Sullivan, Dennis, String topology. arxiv:9911159.Google Scholar
Chataur, David and Le Borgne, Jean-François, On the loop homology of complex projective spaces . Bull. Soc. Math. France 139(2011), no. 4, 503–518. https://doi.org/10.24033/bsmf.2616.Google Scholar
Chataur, David and Menichi, Luc, String topology of classifying spaces . J. Reine Angew. Math. 669(2012), 1–45. https://doi.org/10.1515/CRELLE.2011.140.Google Scholar
Earle, Clifford J. and Eells, James, Teichmüller theory for surfaces with boundary . J. Differential Geometry 4(1970), 169–185. https://doi.org/10.4310/jdg/1214429381.Google Scholar
Farb, Benson and Margalit, Dan, A primer on mapping class groups . Princeton Mathematical Series, 49. Princeton University Press, Princeton, NJ, 2012.Google Scholar
Félix, Yves, Halperin, Stephen, and Thomas, Jean-Claude, Rational homotopy theory . Graduate Texts in Mathematics, 205. Springer-Verlag, New York, 2001. https://doi.org/10.1007/978-1-4613-0105-9.Google Scholar
Félix, Yves, Menichi, Luc, and Thomas, Jean-Claude, Gerstenhaber duality in Hochschild cohomology . J. Pure Appl. Algebra 199(2005), no. 1–3, 43–59. https://doi.org/10.1016/j.jpaa.2004.11.004.Google Scholar
Félix, Yves and Thomas, Jean-Claude, Rational BV-algebra in string topology . Bull. Soc. Math. France 136(2008), no. 2, 311–327. https://doi.org/10.24033/bsmf.2558.Google Scholar
Félix, Yves and Thomas, Jean-Claude, String topology on Gorenstein spaces . Math. Ann. 345(2009), no. 2, 417–452. https://doi.org/10.1007/s00208-009-0361-5.Google Scholar
Freed, Daniel S., Hopkins, Michael J., and Teleman, Constantin, Loop groups and twisted K-theory III . Ann. of Math. (2) 174(2011), no. 2, 947–1007. https://doi.org/10.4007/annals.2011.174.2.5.Google Scholar
Godin, Véronique, Higher string topology operations. arxiv:0711.4859.Google Scholar
Grodal, Jesper and Lahtinen, Anssi, String topology of finite groups of lie type. http://www.math.ku.dk/∼jg/papers/stringtoplie.pdf, July2017.Google Scholar
Halperin, Stephen, Universal enveloping algebras and loop space homology . J. Pure Appl. Algebra 83(1992), no. 3, 237–282. https://doi.org/10.1016/0022-4049(92)90046-I.Google Scholar
Hamstrom, Mary-Elizabeth, Homotopy groups of the space of homeomorphisms on a 2-manifold . Illinois J. Math. 10(1966), 563–573.Google Scholar
Hepworth, Richard, String topology for complex projective spaces. 2009. arxiv:0908.1013.Google Scholar
Hepworth, Richard, String topology for Lie groups . J. Topol. 3(2010), no. 2, 424–442. https://doi.org/10.1112/jtopol/jtq012.Google Scholar
Hepworth, Richard and Lahtinen, Anssi, On string topology of classifying spaces . Adv. Math. 281(2015), 394–507. https://doi.org/10.1016/j.aim.2015.03.022.Google Scholar
Iwase, Norio, Adjoint action of a finite loop space . Proc. Amer. Math. Soc. 125(1997), no. 9, 2753–2757. https://doi.org/10.1090/S0002-9939-97-03924-5.Google Scholar
Johnson, Dennis L., Homeomorphisms of a surface which act trivially on homology . Proc. Amer. Math. Soc. 75(1979), no. 1, 119–125. https://doi.org/10.2307/2042686.Google Scholar
Keller, Bernhard, Deformation quantization after Kontsevich and Tamarkin . In: Déformation, quantification, théorie de Lie . Panor. Synthèses, 20. Soc. Math. France, Paris, 2005, pp. 19–62.Google Scholar
Kishimoto, Daisuke and Kono, Akira, On the cohomology of free and twisted loop spaces . J. Pure Appl. Algebra 214(2010), no. 5, 646–653. https://doi.org/10.1016/j.jpaa.2009.07.006.Google Scholar
Kock, Joachim, Frobenius algebras and 2D topological quantum field theories . London Mathematical Society Student Texts, 59. Cambridge University Press, Cambridge, 2004.Google Scholar
Kono, Akira and Kuribayashi, Katsuhiko, Module derivations and cohomological splitting of adjoint bundles . Fund. Math. 180(2003), no. 3, 199–221. https://doi.org/10.4064/fm180-3-1.Google Scholar
Kupers, Alexander, String topology operations. Master’s thesis, Utrecht University, The Netherlands, 2011.Google Scholar
Kuribayashi, Katsuhiko, Module derivations and the adjoint action of a finite loop space . J. Math. Kyoto Univ. 39(1999), no. 1, 67–85. https://doi.org/10.1215/kjm/1250517954.Google Scholar
Kuribayashi, Katsuhiko, Menichi, Luc, and Naito, Takahito, Derived string topology and the Eilenberg-Moore spectral sequence . Israel J. Math. 209(2015), no. 2, 745–802. https://doi.org/10.1007/s11856-015-1236-y.Google Scholar
Lahtinen, Anssi, Higher operations in string topology of classifying spaces . Math. Ann. 368(2017), no. 1-2, 1–63. https://doi.org/10.1007/s00208-016-1406-1.Google Scholar
McCleary, John, A user’s guide to spectral sequences Second ed., Cambridge Studies in Advanced Mathematics, 58, Cambridge University Press, Cambridge, 2001.Google Scholar
Menichi, Luc, The cohomology ring of free loop spaces . Homology Homotopy Appl. 3(2001), no. 1, 193–224. https://doi.org/10.4310/HHA.2001.v3.n1.a9.Google Scholar
Menichi, Luc, On the cohomology algebra of a fiber . Algebr. Geom. Topol. 1(2001), 719–742. https://doi.org/10.2140/agt.2001.1.719.Google Scholar
Menichi, Luc, String topology for spheres . Comment. Math. Helv. 84(2009), no. 1, 135–157. https://doi.org/10.4171/CMH/155.Google Scholar
Menichi, Luc, A Batalin-Vilkovisky algebra morphism from double loop spaces to free loops . Trans. Amer. Math. Soc. 363(2011), no. 8, 4443–4462. https://doi.org/10.1090/S0002-9947-2011-05374-2.Google Scholar
Milnor, John W. and Moore, John C., On the structure of Hopf algebras . Ann. of Math. (2) 81(1965), 211–264. https://doi.org/10.2307/1970615.Google Scholar
Milnor, John W. and Stasheff, James D., Characteristic classes . Annals of Mathematics Studies, 76, Princeton University Press, Princeton, NJ, 1974.Google Scholar
Mimura, Mamoru and Toda, Hirosi, Topology of Lie groups. I, II . Translations of Mathematical Monographs, 91. American Mathematical Society, Providence, RI, 1991.Google Scholar
Spanier, Edwin H., Algebraic topology . Springer-Verlag, New York, 1981.Google Scholar
Stasheff, James and Halperin, Steve, Differential algebra in its own rite . In: Proceedings of the Advanced Study Institute on Algebraic Topology, vol. 3 . Mat. Inst., Aarhus Univ., Aarhus, 1970, pp. 567–577.Google Scholar
Tamanoi, Hirotaka, Batalin-Vilkovisky Lie algebra structure on the loop homology of complex Stiefel manifolds . Int. Math. Res. Not. (2006), 1–23. https://doi.org/10.1155/IMRN/2006/97193.Google Scholar
Tamanoi, Hirotaka, Cap products in string topology . Algebr. Geom. Topol. 9(2009), no. 2, 1201–1224. https://doi.org/10.2140/agt.2009.9.1201.Google Scholar
Tamanoi, Hirotaka, Stable string operations are trivial . Int. Math. Res. Not. IMRN (2009), no. 24, 4642–4685. https://doi.org/10.1093/imrn/rnp104.Google Scholar
Tamanoi, Hirotaka, Loop coproducts in string topology and triviality of higher genus TQFT operations . J. Pure Appl. Algebra 214(2010), no. 5, 605–615. https://doi.org/10.1016/j.jpaa.2009.07.011.Google Scholar
Tezuka, Michishige, On the cohomology of finite chevalley groups and free loop spaces of classifying spaces. Suurikenkoukyuuroku, 1057:54–55, 1998. http://hdl.handle.net/2433/62316.Google Scholar
Wahl, Nathalie, Ribbon braids and related operads. Ph.D. thesis, Oxford University, 2001. http://www.math.ku.dk/∼wahl/.Google Scholar
Westerland, Craig, String homology of spheres and projective spaces . Algebr. Geom. Topol. 7(2007), 309–325. https://doi.org/10.2140/agt.2007.7.309.Google Scholar
Yang, Tian, A Batalin-Vilkovisky algebra structure on the Hochschild cohomology of truncated polynomials . Topology Appl. 160(2013), no. 13, 1633–1651. https://doi.org/10.1016/j.topol.2013.06.010.Google Scholar