Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T01:30:38.434Z Has data issue: false hasContentIssue false
  • English
  • Français

A Basically Disconnected Normal Space Φ With |βΦ – Φ| = 1

Published online by Cambridge University Press:  20 November 2018

Eric K. van Douwen
Eric K. van Douwen*
Affiliation:
Ohio University, Athens, Ohio
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

All spaces considered are completely regular. C*(X) denotes the set of bounded continuous real-valued functions in X. A subspace S of X is called C*-embedded in X if for every f ∈ C*(S) there is ϕ ∈ C*(X) with ϕ⥤S = f.

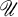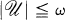A space X is called almost compact if |βX – X| ≦ 1; basically disconnected if every cozero-set has open closure; extremally disconnected if every open set has open closure; an F-space if every cozero-set is C*-embedded; small if |C*(X)| = 2ω; and weakly Lindelöf if every open cover has a subfamily with and ⋃ 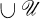dense. A point p of a space X is called a P-point of X if every Gδ-set in X which contains p is a neighborhood of p.

ω(X) denotes the weight of X.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 5 , 01 October 1979 , pp. 911 - 914
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. van Douwen, E. K. and van Mill, J., Parovicenko's characterization of βω-ω implies CH, Proc. Amer. Math. Soc. 72 (1978), 539–541.Google Scholar
2. Fine, N. J. and Gillman, L., Extension of continuous functions in βN, Bull. AM. 66 (1960), 376–381.Google Scholar
3. Gillman, L. and Jerison, M., Rings of continuous functions (Van Nostrand, Princeton, N.J., 1960).Google Scholar
4. Kunen, K., An extremally disconnected space, Notices AMS, 24 (1977), A–263.Google Scholar
5. Kunen, K. and Parsons, L., Projective covers of ordinal spaces, Top. Proc. 3 (1978), 407–428.Google Scholar
6. Woods, R. G., Characterizations of some C*-embedded subspaces of βN, Pacific J. Math. 65 (1976), 573–579.Google Scholar
7. Woods, R. G., The structure of small normal F-spaces, Top. Proc. 1 (1976), 173–179.Google Scholar