Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-29T07:19:25.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Basic Objects for an Algebraic Homotopy Theory

Published online by Cambridge University Press:  20 November 2018

Paul Cherenack
Paul Cherenack*
Affiliation:
Indiana University, Bloomington, Indiana
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purposes of this paper are:

(A) To show (§§ 1, 3, 5) that some of the usual notions of homotopy theory (sums, quotients, suspensions, loop functors) exist in the category 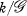of affine k-schemes where the affine rings are countably generated.

(B) By example to demonstrate some of the more geometric relations between two objects of 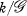and their quotient or to study the algebraic suspension of one of them. See §§ 2.1, 2.2, 2.3, 3.

(C) To prove (§4) that the algebraic suspension (in R/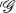) of the n-sphere is homeomorphic to the n + 1 sphere for the usual topologies.

(D) To show that the algebraic loop functor is right adjoint to the algebraic suspension functor (§5).

These results can be viewed as a precursor of definitions for an algebraic homotopy theory from a “geometric” point of view (rather than a more algebraic standpoint employing Galois theory [5]).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 24 , Issue 1 , February 1972 , pp. 155 - 166
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Frost, P., Curve tracing (Chelsea, New York, 1960).Google Scholar
2. Grothendieck, A., Elements de geometrie algebrique. I (Springer-Verlag, Berlin, 1970).Google Scholar
3. Lang, S., Hilbert's Nullstellensatz in infinite dimensional space, Proc. Amer. Math. Soc. 3 (1952), 407–410.Google Scholar
4. Mitchell, B., Theorey of Categories (Academic Press, New York, 1965).Google Scholar
5. Popp, H., Fundamentalgruppen algebraischen Mannigfaltigkeiten (Springer-Verlag, Berlin, 1970).Google Scholar
6. Seidenberg, A., Elements of the theory of algebraic curves (Addison-Wesley, Reading, Massachusetts, 1968).Google Scholar
7. Serre, J. P., Groupes algebrique et corps de classes (Hermann, Paris, 1958).Google Scholar
8. Walker, R., Algebraic curves (Dover, New York, 1950).Google Scholar