Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kalton, N. J.
and
Montgomery-Smith, S. J.
1993.
Set-functions and factorization.
Archiv der Mathematik,
Vol. 61,
Issue. 2,
p.
183.
Guédon, O.
and
Litvak, A. E.
2000.
Geometric Aspects of Functional Analysis.
Vol. 1745,
Issue. ,
p.
95.
2003.
Foundations of Complex Analysis in Non Locally Convex Spaces - Function Theory Without Convexity Condition.
Vol. 193,
Issue. ,
p.
261.
Bayoumi, Aboubakr
2003.
Foundations of Complex Analysis in Non Locally Convex Spaces - Function Theory Without Convexity Condition.
Vol. 193,
Issue. ,
p.
227.
Albiac, F.
Kalton, N.
and
Leránoz, C.
2004.
Uniqueness of the Unconditional Basis of ℓ1 (ℓp) and ℓp (ℓ1), 0 < p < 1.
Positivity,
Vol. 8,
Issue. 4,
p.
443.
Albiac, F.
and
Leránoz, C.
2008.
Uniqueness of symmetric basis in quasi-Banach spaces.
Journal of Mathematical Analysis and Applications,
Vol. 348,
Issue. 1,
p.
51.
Albiac, Fernando
and
Leránoz, Camino
2010.
Uniqueness of unconditional basis in quasi-Banach spaces which are not sufficiently Euclidean.
Positivity,
Vol. 14,
Issue. 4,
p.
579.
Albiac, F.
and
Leránoz, C.
2011.
Uniqueness of unconditional bases in nonlocally convex ℓ1-products.
Journal of Mathematical Analysis and Applications,
Vol. 374,
Issue. 2,
p.
394.
Albiac, F.
and
Leránoz, C.
2011.
Uniqueness of unconditional bases in nonlocally convex c0-products.
Israel Journal of Mathematics,
Vol. 184,
Issue. 1,
p.
79.
Godefroy, G.
2014.
Obituary: Nigel John Kalton, 1946–2010.
Bulletin of the London Mathematical Society,
Vol. 46,
Issue. 6,
p.
1292.
Albiac, Fernando
and
Ansorena, José Luis
2015.
On the mutually non isomorphic ℓp(ℓq) spaces, II.
Mathematische Nachrichten,
Vol. 288,
Issue. 1,
p.
5.
Motos, Joaquín
Planells, María Jesús
and
Talavera, César F.
2015.
Duals of variable exponent Hörmander spaces ( $$0< p^- \le p^+ \le 1$$ 0 < p - ≤ p + ≤ 1 ) and some applications.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 109,
Issue. 2,
p.
657.
Czerwińska, M. M.
and
Kamińska, A.
2017.
Banach envelopes in symmetric spaces of measurable operators.
Positivity,
Vol. 21,
Issue. 1,
p.
473.
Albiac, Fernando
and
Ansorena, José Luis
2017.
Isomorphic classification of mixed sequence spaces and of Besov spaces over [0, 1]d.
Mathematische Nachrichten,
Vol. 290,
Issue. 8-9,
p.
1177.
Albiac, Fernando
and
Ansorena, José Luis
2021.
Projections and unconditional bases in direct sums of ℓp spaces, 0<p≤∞.
Mathematische Nachrichten,
Vol. 294,
Issue. 11,
p.
2052.
Albiac, Fernando
Ansorena, José L.
and
Wojtaszczyk, Przemysław
2021.
On a ‘philosophical’ question about Banach envelopes.
Revista Matemática Complutense,
Vol. 34,
Issue. 3,
p.
747.
Albiac, Fernando
Ansorena, José L.
Cúth, Marek
and
Doucha, Michal
2022.
Structure of the Lipschitz free p-spaces $${\mathcal{F}}_p({\mathbb{Z}}^d)$$ and $${\mathcal{F}}_p({\mathbb{R}}^d)$$ for $$0<p\le 1$$.
Collectanea Mathematica,
Vol. 73,
Issue. 3,
p.
337.
Muratov, M. A.
and
Rubshtein, B.-Z. A.
2022.
Symmetric Spaces of Measurable Functions: Some New and Old Advances.
Journal of Mathematical Sciences,
Vol. 265,
Issue. 6,
p.
924.
Albiac, Fernando
Ansorena, José L.
and
Wojtaszczyk, Przemysław
2022.
Uniqueness of unconditional basis of Hp(T)⊕ℓ2 and Hp(T)⊕T(2) for 0 < p < 1.
Journal of Functional Analysis,
Vol. 283,
Issue. 7,
p.
109597.
Albiac, F.
and
Ansorena, J. L.
2022.
Addendum to “uniqueness of unconditional basis of infinite direct sums of quasi-Banach spaces”.
Positivity,
Vol. 26,
Issue. 5,


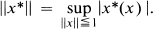
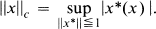
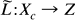 .
.