Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T01:13:22.964Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphisms of G-Azumaya Algebras

Published online by Cambridge University Press:  20 November 2018

Margaret Beattie
Margaret Beattie*
Affiliation:
Mount Saint Vincent University, Halifax, Nova Scotia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a commutative ring, G a finite abelian group of order n and exponent m, and assume n is a unit in R. In [10], F. W. Long defined a generalized Brauer group, BD(R, G), of algebras with a G-action and G-grading, whose elements are equivalence classes of G-Azumaya algebras. In this paper we investigate the automorphisms of a G-Azumaya algebra A and prove that if Picm(R) is trivial, then these automorphisms are all, in some sense, inner.

In fact, each of these “inner” automorphisms can be written as the composition of an inner automorphism in the usual sense and a “linear“ automorphism, i.e., an automorphism of the type

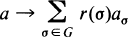
with r(σ) a unit in R. We then use these results to show that the group of gradings of the centre of a G-Azumaya algebra A is a direct summand of G, and thus if G is cyclic of order pr, A is the (smash) product of a commutative and a central G-Azumaya algebra.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 6 , 01 December 1985 , pp. 1047 - 1058
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Bass, H., Lectures on topics in algebraic K-theory, Tata Institute for Fundamental Research, Bombay (1967).Google Scholar
2. Beattie, M., A direct sum decomposition for the Brauer group of H-module algebras, J. Algebra 43 (1976), 686–693.Google Scholar
3. Beattie, M., The Brauer group of central separable G-Azumaya algebras, J. Algebra 54 (1978), 516–525.Google Scholar
4. Childs, L. N., The Brauer group of graded algebras II. Graded Galois extensions, Trans. Amer. Math. Soc. 204 (1975), 137–160.Google Scholar
5. Childs, L. N., Garfinkel, G. and Orzech, M., The Brauer group of graded Azumaya algebras, Trans. Amer. Math. Soc. 175 (1973), 299–325.Google Scholar
6. Deegan, A. P., A subgroup of the generalized Brauer group of Γ-Azumaya algebras, J. London Math. Soc. (1981), 223–240.Google Scholar
7. DeMeyer, F. and Ingraham, E., Separable algebras over commutative rings, Lecture Notes in Mathematics 181 (Springer-Verlag, Berlin, 1971).CrossRefGoogle Scholar
8. Laborde, M. O., Théorème de Skolem-Nother pour les algèbres d'Azumaya graduées sur un anneau semi-local, C. R. Acad. Se. Paris, Série A 279 (1974), 447–449.Google Scholar
9. Long, F. W., The Brauer group of dimodule algebras, J. Algebra 30 (1974), 559–601.Google Scholar
10. Long, F. W., A generalization of the Brauer group of graded algebras, Proc. London Math. Soc. 29 (1974), 237–256.Google Scholar
11. Nakajima, A., Some results on H-Azumaya algebras, Math. J. Okayama Univ. 19 (1977), 101–110.Google Scholar
12. Orzech, M., On the Brauer group of modules having a grading and an action, Can. J. Math. 25 (1976), 533–552.Google Scholar
13. Orzech, M., Correction to “On the Brauer group of algebras having a grading and an action'\ Can. J. Math. 32 (1980), 1523–1524.Google Scholar
14. Sweedler, M. E., Uopf algebras (Benjamin, New York, 1969).Google Scholar