Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-11T03:45:32.218Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphismes modérés de l'espace affine

Published online by Cambridge University Press:  20 November 2018

Eric Edo
Eric Edo*
Affiliation:
Département de mathématiques pures, Université Bordeaux I, 351, cours de la Libération, 33405 Talence Cedex, FRANCE e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Le problème de Jung-Nagata 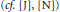$\left( cf.\,\left[ \text{J} \right],\,\left[ \text{N} \right] \right)$ consiste à savoir s'il existe des automorphismes de 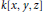$k\left[ x,\,y,\,z \right]$ qui ne sont pas modérés. Nous proposons une approche nouvelle de cette question, fondée sur l'utilisation de la théorie des automates et du polygone de Newton. Cette approche permet notamment de généraliser de façon significative les résultats de 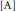$\left[ \text{A} \right]$.

Abstract

Abstract

The Jung-Nagata's problem 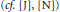$\left( cf.\,\left[ \text{J} \right],\,\left[ \text{N} \right] \right)$ asks if there exists non-tame (or wild) automorphisms of 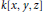$k\left[ x,\,y,\,z \right]$. We give a new way to attack this question, based on the automata theory and the Newton polygon. This new approch allows us to generalize significantly the results of 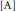$\left[ \text{A} \right]$.

Keywords

14R10tame automorphismsautomataNewton polygon
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 3 , 01 June 2003 , pp. 533 - 560
Copyright
Copyright © Canadian Mathematical Society 2003

References

Références

[A] Alev, J., A note on Nagata's automorphism. Dans: Automorphisms of the affine spaces (ed. A. van den Essen), Kluwer Academic Publishers, 1995, 215–221.Google Scholar
[DGY] Drensky, V., Gutierrez, J. and Yu, J.-T. Gröbner bases and the Nagata automorphism. J. Pure Appl. Algebra (2) 135(1999), 135–153.Google Scholar
[E] van den Essen, A., Polynomial automorphisms and the Jacobian Conjecture. Progr. Math. 190, Birkhäuser Verlag, Basel-Boston-Berlin, 2000.Google Scholar
[EV] Edo, E. and Vénéreau, S. Length 2 variables and transfer. Ann. Polon. Math. 76(2001), 67–76.Google Scholar
[Fr] Freudenburg, G. Triangulability criteria for additive group actions on affine space. J. Pure Appl. Algebra (3) 105(1995), 267–275.Google Scholar
[Fu] Furter, J-P. On the variety of automorphisms of the affine plane. J. Algebra (2) 195(1997), 604–623.Google Scholar
[FM] Friedland, S. and Milnor, J. Dynamical properties of plane polynomial automorphisms. Ergodic Theory Dynamical Systems (1) 9(1989), 67–99.Google Scholar
[J] Jung, H. Über ganze birationale Transformationen der Ebene. J. Reine Angew.Math. 184(1942), 161–174.Google Scholar
[Ko] Kozen, D., Automata and computability. Undergraduate Texts in Computer Science, Springer-Verlag, New York, 1997.Google Scholar
[Ku] van der Kulk, W. On polynomial rings in two variables. Nieuw Arch. Wiskunde (3) 1(1953), 33–41.Google Scholar
[Lak] Lakatos, I., Preuves et réfutations, essai sur la logique de la découverte mathématique. Hermann, Paris, 1984.Google Scholar
[Lam] Lamy, S., Automorphismes polyn.omiaux du plan complexe : étude algébrique et dynamique. Thèse de doctorat, Univ. Paul Sabatier, Toulouse, 2000.Google Scholar
[LB] Le Bruyn, L. Automorphisms and Lie stacks. Comm. Algebra (7) 25(1997), 2211–2226.Google Scholar
[MT] Mneimnét, R. et Testard, F., Introduction à la théorie des groupes de Lie classiques. Collection Méthodes, Hermann, Paris, 1986.Google Scholar
[N] Nagata, M., On the automorphisms group of C[X,Y]. Lectures in Math. Kyoto Univ. 5, 1972.Google Scholar
[R] Russell, P. Simple birational extensions of two dimensional affine rational domains. Compositio Math. (2) 33(1976), 197–208.Google Scholar