Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T00:58:47.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphism Groups of Denumerable Boolean Algebras

Published online by Cambridge University Press:  20 November 2018

Ralph Mckenzie
Ralph Mckenzie*
Affiliation:
University of California, Berkeley, California
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

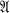We are concerned with the extent to which the structure of a Boolean algebra (or BA, for brevity) is reflected in its group of automorphisms, Aut 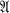. In particular, for which algebras can one conclude that if 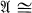Aut Aut 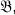, then 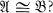Monk has conjectured [3] that this implication holds for denumerable BA's with at least one atom. We shall refute his conjecture, but show that the implication does hold if 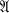and 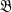are denumerable, if each has at least one atom, and if the sum of the atoms exists in 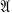. In fact, under those assumptions the algebra 21 can be rather neatly recovered from its abstract automorphism group.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 29 , Issue 3 , 01 June 1977 , pp. 466 - 471
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. McKenzie, R., On elementary types of symmetric groups, Algebra Universalis 1 (1971), 13–20.Google Scholar
2. McKenzie, R. and Monk, J. D., On automorphism groups of Boolean algebras, to appear in proceedings of the International Colloquium of Infinite and Finite Sets, Keszthely, Hungary, 1973.Google Scholar
3. Monk, J. D., On the automorphism groups of denumerable Boolean algebras, submitted to Math. Annalen.Google Scholar
4. Rubin, M., On the automorphism groups of saturated atomic Boolean algebras, to appear, Algebra Universalis.Google Scholar