Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T21:11:29.921Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotics for Functions Associated with Heat Flow on the Sierpinski Carpet

Published online by Cambridge University Press:  20 November 2018

B. M. Hambly
B. M. Hambly*
Affiliation:
Mathematical Institute, University of Oxford, Oxford, U.K. email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

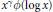We establish the asymptotic behaviour of the partition function, the heat content, the integrated eigenvalue counting function, and, for certain points, the on-diagonal heat kernel of generalized Sierpinski carpets. 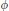For all these functions the leading term is of the form $ {{x}^{\text{ }\!\!\gamma\!\!\text{ }}}\phi \left( \log x \right)$ for a suitable exponent $\text{ }\!\!\gamma\!\!\text{ }$ and $\phi $ a periodic function. We also discuss similar results for the heat content of affine nested fractals.

Keywords

35K0528A8035B4060J65
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 1 , 01 February 2011 , pp. 153 - 180
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Barlow, M. T., Diffusions on fractals, In: Lectures in Probability Theory and Statistics: Ecole d'ètè de probabilitès de Saint-Flour XXV, Lect. Notes Math., 1690, Springer, New York, 1998.Google Scholar
[2] Barlow, M. T. and Bass, R. F., The construction of Brownian motion on the Sierpiński carpet. Ann Inst H. Poincarè Probab. Statist. 25 (1989), no. 3, 225-257.Google Scholar
[3] Barlow, M. T. and Bass, R. F., On the resistance of the Sierpiński carpet. Proc. Roy. Soc. London Ser. A 431 (1990), no. 1882, 345-360. doi:10.1098/rspa.1990.0135Google Scholar
[4] Barlow, M. T. and Bass, R. F., Transition density estimates for Brownian motion on the Sierpiński carpet. Probab. Theory Related Fields 91 (1992), no. 3-4, 307-330. doi:10.1007/BF01192060Google Scholar
[5] Barlow, M. T. and Bass, R. F., Brownian motion and harmonic analysis on Sierpinski carpets. Canad. J. Math. 51 (1999), no. 4, 673-744.Google Scholar
[6] Barlow, M. T., Bass, R. F., Kumagai, T., and Teplyaev, A., Uniqueness of Brownian motion on Sierpiński carpets. J. Eur. Math. Soc. (JEMS) 12 (2010), no. 3, 655-701.Google Scholar
[7] Barlow, M. T. and Kigami, J., Localized eigenfunctions of the Laplacian on p.c.f. self-similar sets. J. London Math. Soc. 56 (1997), no. 2, 320-332. doi:10.1112/S0024610797005358Google Scholar
[8] Barlow, M. T. and Perkins, E. A., Brownian motion on the Sierpiński gasket. Probab. Theory Related Fields 79 (1988), no. 4, 543-623. doi:10.1007/BF00318785Google Scholar
[9] van den Berg, M., Heat content and Brownian motion for some regions with a fractal boundary. Probab. Theory Related Fields 100 (1994), no. 4, 439-456. doi:10.1007/BF01268989Google Scholar
[10] van den Berg, M., Heat equation on the arithmetic von Koch snowflake. Probab. Theory Related Fields 118 (2000), no. 1, 17-36. doi:10.1007/PL00008740Google Scholar
[11] van den, M., Berg and Gilkey, P. B., A comparison estimate for the heat equation with an application to the heat content of the S-adic von Koch snowflake. Bull. London Math. Soc. 30 (1998), no. 4, 404-412. doi:10.1112/S0024609398004469Google Scholar
[12] van den, M., Berg and den Hollander, F., Asymptotics for the heat content of a planar region with a fractal polygonal boundary. Proc. London Math. Soc. 78 (1999), no. 3, 627-661. doi:10.1112/S0024611599001781Google Scholar
[13] Fitzsimmons, P. J., Hambly, B. M., and Kumagai, T., Transition density estimates for Brownian motion on affine nested fractals. Comm. Math. Phys. 165 (1994), no. 3, 595-620. doi:10.1007/BF02099425Google Scholar
[14] Fleckinger, J., Levitin, M., and Vassiliev, D., Heat equation on the triadic von Koch snowflake: asymptotic and numerical analysis. Proc. London Math. Soc. (3) 71 (1995), no. 2, 372-396. doi:10.1112/plms/s3-71.2.372Google Scholar
[15] Fukushima, M. and, Shima, T., On a spectral analysis for the Sierpiński gasket. Potential Anal. 1 (1992), no. 1, 1-35. doi:10.1007/BF00249784Google Scholar
[16] Hambly, B. M., Kumagai, T., Kusuoka, S., and Zhou, X. Y., Transition density estimates for diffusion processes on homogeneous random Sierpinski carpets. J. Math. Soc. Japan 52 (2000), no. 2, 373-408. doi:10.2969/jmsj/05220373Google Scholar
[17] Kajino, N., Spectral asymptotics for Laplacians on self-similar sets. J. Funct. Anal. 258 (2010), no. 4, 1310-1360. doi:10.1016/j.jfa.2009.11.001Google Scholar
[18] Kigami, J., Analysis on fractals. Cambridge Tracts in Mathematics, 143, Cambridge University Press, Cambridge, 2001.Google Scholar
[19] Kigami, J. and, Lapidus, M. L., Weyl's problem for the spectral distribution of Laplacians on p.c.f. self-similar fractals. Commun. Math. Phys. 158 (1993), no. 1, 93-125. doi:10.1007/BF02097233Google Scholar
[20] Kumagai, T., Estimates of transition densities for Brownian motion on nested fractals. Probab. Theory Related Fields 96 (1993), no. 2, 205-224. doi:10.1007/BF01192133Google Scholar
[21] Kumagai, T., Short time asymptotic behaviour and large deviation for Brownian motion on some affine nested fractals. Publ. Res. Inst. Math. Sci. 33 (1997), no. 2, 223-240. doi:10.2977/prims/1195145448 Theory Related Fields 93 (1992), no. 2, 169-196. doi:10.1007/BF01195228Google Scholar
[22] Kusuoka, S. and, Zhou, X. Y., Dirichlet forms on fractals: Poincarè constant and resistance. Probab.Google Scholar
[23] Lau, K- S., Wang, J., and Chu, C- H., Vector-valued Choquet-Deny theorem, renewal equation and self-similar measures. Studia Math. 117 (1995), no. 1, 1-28.Google Scholar
[24] Levitin, M. and, Vassiliev, D., Spectral asymptotics, renewal theorem, and the Berry conjecture for a class of fractals. Proc. London. Math. Soc. 72 (1996), no. 1, 188-214. doi:10.1112/plms/s3-72.1.188Google Scholar
[25] LindstrØm, T., Brownian motion on nested fractals. Mem. Amer. Math. Soc. 83 (1990), no. 420.Google Scholar
[26] Mauldin, R. D. and S. C., Williams, Hausdorff dimension in graph directed constructions. Trans. Amer. Math. Soc. 309 (1988), no. 2, 811-829.Google Scholar
[27] Rammal, R. and, Toulouse, G., Random walks on fractal structures and percolation clusters. J. Physique Lettres 44 (1983), L13-L22.Google Scholar
[28] Sabot, C., Spectral properties of self-similar lattices and iteration of rational maps. Mèm. Soc. Math. Fr. (N. S.) 92 (2003).Google Scholar