Let 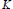$K$ be a convex body in 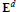${{\mathbf{E}}^{d}}$ and denote by 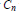${{C}_{n}}$ the set of centroids of $n$ non-overlapping translates of 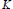$K$. For 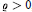$\varrho \,>\,0$, assume that the parallel body conv 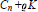${{C}_{n}}\,+\,\varrho K$ of conv 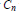${{C}_{n}}$ has minimal volume. The notion of parametric density (see [21]) provides a bridge between finite and infinite packings (see [4] or [14]). It is known that there exists a maximal 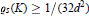${{\varrho }_{s}}(K)\,\ge \,1/(32{{d}^{2}})$ such that conv 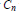${{C}_{n}}$ is a segment for 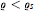$\varrho \,<\,{{\varrho }_{s}}$ (see [5]). We prove the existence of a minimal 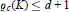${{\varrho }_{c}}(K)\,\le \,d\,+\,1$ such that if 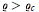$\varrho \,>\,{{\varrho }_{c}}$ and $n$ is large then the shape of conv 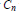${{C}_{n}}$ can not be too far from the shape of 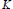$K$. For 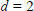$d\,=\,2$, we verify that 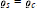${{\varrho }_{s\,}}\,=\,{{\varrho }_{c}}$. For 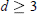$d\,\ge \,3$, we present the first example of a convex body with known 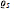${{\varrho }_{s}}$ and 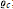${{\varrho }_{c}}$; namely, we have 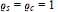${{\varrho }_{s}}\,=\,{{\varrho }_{c}}\,=\,1$ for the parallelotope.