Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
de Oliveira Filho, Fernando Mário
and
Vallentin, Frank
2013.
A quantitative version of Steinhaus’ theorem for compact, connected, rank-one symmetric spaces.
Geometriae Dedicata,
Vol. 167,
Issue. 1,
p.
295.
Naidenov, Nikola
Nikolov, Geno
and
Shadrin, Alexei
2018.
On the Largest Critical Value of $T_n^(k)$.
SIAM Journal on Mathematical Analysis,
Vol. 50,
Issue. 3,
p.
2389.
Ismail, Mourad E. H.
and
Assche, Walter Van
2020.
Encyclopedia of Special Functions: The Askey-Bateman Project.


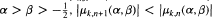 for
for 