Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T09:27:07.506Z Has data issue: false hasContentIssue false
  • English
  • Français

The Asymptotic behaviour Of μ(z, β, α)

Published online by Cambridge University Press:  20 November 2018

M. Wyman  and
R.Wong
M. Wyman
Affiliation:
The University of Alberta, Edmonton, Alberta
R.Wong
Affiliation:
The University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The function μ(z, β, α) defined by

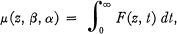
where

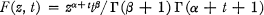
plays an important role in Volterra's theory of convolution-logarithms, and also in the Paley-Wiener inversion formula for the Laplace transformation. These and other properties of pi are briefly described in (3).

Our aim in this paper is to find the asymptotic behaviour of μ as |z| < ∞, a result which, as far as we are aware, has not been obtained. It is of interest to note that the procedure to be used also gives, with some minor modification, the asymptotic behaviour of μ as z → 0, a result that is well known (3, p. 219). When this behaviour becomes known, it becomes possible to write a significant generalization of Watson's Lemma.

In 1906, Barnes (1) published a significant paper containing many asymptotic results of major importance. It is of passing interest to note that this paper contains a general theorem from which the result of Watson's Lemma, published in 1918, can easily be obtained. It would seem that this latter result is misnamed in mathematical literature, and might well be called Barnes’ Lemma.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 1013 - 1023
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Barnes, E. W., The asymptotic expansion of integral functions defined by Taylor's series, Phil. Trans. Roy. Soc. (London), A206 (1906), 249–297.Google Scholar
2. Erdélyi, A., General asymptotic expansions of Laplace integrals, Arch. Rat. Mech. Anal. 7 (1961), 1–20.Google Scholar
3. Erdélyi, A., Magnus, W., Oberhettinger, F., and Tricomi, F. G., Higher transcendental functions, Vol. III ; based in part, on notes by Harry Bateman (McGraw-Hill, New York, 1955).Google Scholar
4. Watson, G. N., Harmonic functions associated with the parabolic cylinder, Proc. London Math. Soc. (2) 17 (1918), 116–148.Google Scholar