Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T00:57:41.293Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic Behaviour of Nonoscillatory Equations

Published online by Cambridge University Press:  20 November 2018

Allan L. Edelson  and
Emilia Perri
Allan L. Edelson
Affiliation:
University of California, Davis, California
Emilia Perri
Affiliation:
Università di Firenze, Firenze, Italia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For nonlinear equations of the form

I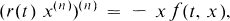

there has been considerable interest in determining the asymptotic forms of nonoscillatory solutions. We assume r(t) is continuous and positive on [0, ∞), and f(t, x) is continuous on [0, ∞) × R, and f(t, x) ≥ 0 for x ≠ 0. For n = 2, equation (I) was studied by Kusano and Naito [3], who found necessary and sufficient conditions for the existence of minimal and maximal nonoscillatory solutions. The former are the bounded solutions, while the later are those asymptotic to the function

1.1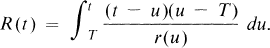

Their method consisted of writing (I) in the form of an integral operator and applying the Schauder fixed point theorem. For arbitrary n, but for r(t) = 1, Kreith [2] found necessary and sufficient conditions for the existence of maximal solutions.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 3 , 01 June 1983 , pp. 436 - 453
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Edelson, A. L. and Schuur, J., Asymptotic behaviour of nth order equations, Pacific J. Math, (to appear).Google Scholar
2. Kreith, K., Extremal solutions for a class of nonlinear differential equations, Proc. Amer. Math. Soc. 79 (1980), 415–421.Google Scholar
3. Kusano, T. and Naito, M., Nonlinear oscillation of fourth order differential equations, Can. J. Math. 28 (1976), 840–852.Google Scholar