Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T12:18:23.118Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic Behavior of the Length of Local Cohomology

Published online by Cambridge University Press:  20 November 2018

Steven Dale Cutkosky ,
Huy Tài Hà ,
Hema Srinivasan  and
Emanoil Theodorescu
Steven Dale Cutkosky
Affiliation:
Department of Mathematics, University of Missouri, Columbia, Missouri, 65201 USA, email: [email protected], [email protected], [email protected], [email protected]
Huy Tài Hà
Affiliation:
Department of Mathematics, University of Missouri, Columbia, Missouri, 65201 USA, email: [email protected], [email protected], [email protected], [email protected]
Hema Srinivasan
Affiliation:
Department of Mathematics, University of Missouri, Columbia, Missouri, 65201 USA, email: [email protected], [email protected], [email protected], [email protected]
Emanoil Theodorescu
Affiliation:
Department of Mathematics, University of Missouri, Columbia, Missouri, 65201 USA, email: [email protected], [email protected], [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

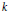Let $k$ be a field of characteristic 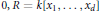$0,\,R\,=\,k\left[ {{x}_{1}},\,\ldots ,\,{{x}_{d}} \right]$ be a polynomial ring, and 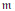$m$ its maximal homogeneous ideal. Let 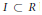$I\,\subset \,R$ be a homogeneous ideal in 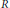$R$. Let 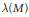$\lambda (M)$ denote the length of an 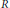$R$-module 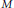$M$. In this paper, we show that

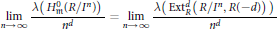$$\underset{x\to \infty }{\mathop{\lim }}\,\,\frac{\lambda \left( H_{m}^{0}\left( R/{{I}^{n}} \right) \right)}{{{n}^{d}}}\,=\,\underset{x\to \infty }{\mathop{\lim }}\,\,\frac{\lambda \left( \text{Ext}_{R}^{d}\left( R/{{I}^{n}},\,R\left( -d \right) \right) \right)}{{{n}^{d}}}$$

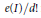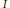always exists. This limit has been shown to be $e(I)/d!$ for $m$-primary ideals $I$ in a local Cohen–Macaulay ring, where 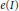$e(I)$ denotes the multiplicity of 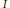$I$. But we find that this limit may not be rational in general. We give an example for which the limit is an irrational number thereby showing that the lengths of these extension modules may not have polynomial growth.

Keywords

13D4014B1513D45powers of idealslocal cohomologyHilbert functionlinear growth
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 6 , 01 December 2005 , pp. 1178 - 1192
Copyright
Copyright © Canadian Mathematical Society 2005

References

[BH] Bruns, W. and Herzog, J., Cohen–Macaulay rings. Cambridge Studies in Advanced Math. 39, Cambridge University Press, Cambridge.Google Scholar
[Ch] Chandler, K. A., Regularity of the powers of an ideal. Comm. Algebra. 25(1997), 3773–3776.Google Scholar
[CHTV] Conca, A., Herzog, J., Trung, N. V. and Valla, G., Diagonal subalgebras of bi-graded algebras and embeddings of blow-ups of projective spaces. Amer. J. Math. 119(1997), 859–901.Google Scholar
[Cu] Cutkosky, S. D., Irrational asymptotic behaviour of Castelnuovo–Mumford regularity. J. Reine Angew.Math. 522(2000), 93–103.Google Scholar
[CEL] Cutkosky, S. D., Ein, L. and Lazarsfeld, R., Positivity and complexity of ideal sheaves. Math. Ann. 321(2001), 213–234.Google Scholar
[CHT] Cutkosky, S. D., Herzog, J. and Trung, N. V., Asymptotic behaviour of the Castenuovo–Mumford regularity. Compositio Math. 118(1999), 243–261.Google Scholar
[Fu] Fujita, T., Approximating Zariski decomposition of big line bundles. Kodai Math. J. 17(1994), 1–3.Google Scholar
[F2] Fujita, T., Semipositive line bundles. J. of the Faculty of Science, The University of Tokyo 30(1983), 353–378.Google Scholar
[GGP] Geramita, A. V., Gimigliano, A. and Pitteloud, Y., Graded Betti numbers of some embedded rational n-folds. Math. Ann. 301(1995), 363–380.Google Scholar
[HaT] Tài Hà, H. and Trung, N. V., Arithmetic Cohen–Macaulayness of blow-ups. preprint.Google Scholar
[H] Hartshorne, R.. Algebraic Geometry. Graduate Texts in Math. 52, Springer Verlag, Berlin, Heidelberg, 1977.Google Scholar
[HoH] Hoa, L. T. and Hyry, E., On local cohomology and Hilbert function of powers of ideals. Manuscripta Math. 112(2003), 77–92.Google Scholar
[HgT] Hoang, N. D. and Trung, N. V., Hilbert polynomials of non-standard bigraded algebras. Math. Z. 245(2003), 304–334.Google Scholar
[I] Iitaka, S., Algebraic Geometry. Graduate Texts in Math. 76, Springer Verlag, New York, Heidelberg, Berlin.Google Scholar
[Ki] Kirby, D., Hilbert functions and the extension functor.Math. Proc. Cambridge Philos. Soc. (3) 105(1989), 441–446.Google Scholar
[Ko1] Kodiyalam, V., Homological invariants of powers of an ideal. Proc. Amer.Math. Soc. (3) 118(1993), 757–764.Google Scholar
[Ko2] Kodiyalam, V., Asymptotic behaviour of Castelnuovo–Mumford regularity. Proc. Amer.Math. Soc. (2) 128(2000), 407–411.Google Scholar
[La] Lazarsfeld, R., Positivity in Algebraic Geometry. Springer-Verlag, Berlin, 2004.Google Scholar
[M] McAdam, S., Asymptotic prime divisors and analytic spreads. Proc. Amer. Math. Soc. 80(1980), 555–559.Google Scholar
[STV] Simis, A., Trung, N. V. and Valla, G., The diagonal subalgebra of a blow-up algebra. J. Pure Appl. Algebra. (1–3) 125(1998), 305–328.Google Scholar
[S] Swanson, I., Powers of ideals: Primary decompositions, Artin–Rees Lemma and Regularity. Math. Ann. 307(1997), 299–313.Google Scholar
[Th] Theodorescu, E., Derived functors and Hilbert polynomials. Math. Proc. Cambridge Philos. Soc. 132(2002), 75–88.Google Scholar
[Th2] Theodorescu, E., Derived functors and Hilbert polynomials. University of Kansas thesis, 2002.Google Scholar