Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T00:28:36.440Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation by Unimodular Functions

Published online by Cambridge University Press:  20 November 2018

Stephen Fisher
Stephen Fisher*
Affiliation:
Northwestern University, Evanston, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The theorems in this paper are all concerned with either pointwise or uniform approximation by functions which have unit modulus or by convex combinations of such functions. The results are related to, and are outgrowths of, the theorems in [4; 5; 10].

In § 1, we show that a function bounded by 1, which is analytic in the open unit disc Δ and continuous on 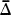may be approximated uniformly on the set where it has modulus 1 (subject to certain restrictions; see Theorem 1) by a finite Blaschke product; that is, by a function of the form

*

where |λ| = 1 and |αi| < 1, i = 1, …, N. In § 1 we also discuss pointwise approximation by Blaschke products with restricted zeros.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 2 , April 1971 , pp. 257 - 269
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Ahern, P. R. and Clark, D. N., Radial limits and invariant subspaces, Amer. J. Math. 92 (1970), 332–342.Google Scholar
2. Carathéodory, C., Theory of functions of a complex variable, Vol. 2, Translated by Steinhardt, F. (Chelsea, New York, 1954).Google Scholar
3. Carleson, L., A representation formula for the Dirichlet integral, Math. Z. 73 (1960), 190–196.Google Scholar
4. Fisher, S., The convex hull of the finite Blaschke products, Bull Amer. Math. Soc. 74 (1968), 1128–1129.Google Scholar
5. Fisher, S., Another theorem on convex combinations of unimodular functions, Bull. Amer. Math. Soc. 75 (1969), 1037–1039.Google Scholar
6. Frostman, O., Potentiel d'équilibre et capacité des ensembles avec quelque applications à la théorie des fonctions, Medd. Lunds Univ. Mat. Sem. 3 (1935), 1–118.Google Scholar
7. Helson, H. and Sarason, D., Past and future, Math. Scand. 21 (1967), 5–16.Google Scholar
8. Hoffman, K., Banach spaces of analytic functions, Prentice-Hall Series in Modern Analysis (Prentice-Hall, Englewood Cliffs, N. J., 1962).Google Scholar
9. Phelps, R. R., Extreme points in function algebras, Duke Math. J. 32 (1965), 267–278.Google Scholar
10. Rudin, W., Convex combinations of unimodular functions, Bull. Amer. Math. Soc. 76 (1969), 795–797.Google Scholar
11. Rudin, W., Function theory in poly discs (Benjamin, New York, 1969).Google Scholar