Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T01:15:58.397Z Has data issue: false hasContentIssue false
  • English
  • Français

Anisotropic Sobolev Capacity withFractional Order

Published online by Cambridge University Press:  20 November 2018

Jie Xiao  and
Deping Ye
Jie Xiao
Affiliation:
Department of Mathematics and Statistics, Memorial University, St. John's, NL A1c 5S7, Canada e-mail: [email protected]
Deping Ye
Affiliation:
Department of Mathematics and Statistics, Memorial University, St. John's, NL A1C 5S7, Canada e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we introduce the anisotropic Sobolev capacity with fractional order and develop some basic properties for this new object. Applications to the theory of anisotropic fractional Sobolev spaces are provided. In particular, we give geometric characterizations for a nonnegative Radon measure 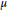$\mu $ that naturally induces an embedding of the anisotropic fractional Sobolev class 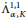$\dot{\Lambda }_{\alpha ,K}^{1,1}$ into the 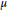$\mu $-based-Lebesgue-space 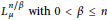$L_{\mu }^{n/\beta }\,\text{with}\,0<\beta \le n$. Also, we investigate the anisotropic fractional $\alpha $-perimeter. Such a geometric quantity can be used to approximate the anisotropic Sobolev capacity with fractional order. Estimation on the constant in the related Minkowski inequality, which is asymptotically optimal as 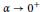$\alpha \to {{0}^{+}}$, will be provided.

Keywords

52A3853A1553A30sharpnessisoperimetric inequalityMinkowski inequalityfractional Sobolev capacityfractional perimeter
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 4 , 01 August 2017 , pp. 873 - 889
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Adams, D. R., Besov capacity redux. J. Math. Sci. (N.Y.) 162 (2009), no. 3, 307–318.http://dx.doi.org/10.1007/s10958-009-9639-0 Google Scholar
[2] Adams, D. R. and Xiao, J., Strong type estimates for homogeneous Besov capacities. Math. Ann. 325(2003), no. 4, 695–709.http://dx.doi.org/10.1007/s00208-002-0396-3 Google Scholar
[3] Bourgain, J., Brezis, H., and Mironescu, P., Another look at Sobolev spaces. In: Optimal control and partial differential equations, J. L.|Menaldi, E.|Rofman, and A.|Sulem, eds. a volume in honour of A. Bensoussan's 60th birthday, IOS Press, 2001, pp. 439–455.Google Scholar
[4] Bourgain, J., Brezis, H. and Mironescu, P., Limiting embedding theorems for Ws,p when and applications. J. Anal. Math. 87(2002), 77–101.http://dx.doi.Org/10.1007/BF02868470 Google Scholar
[5] Di Nezza, E., G.|Palatucci, and E.|Valdinoci, Hichhiker-s guide to the fractional Sobolev spaces. Bull. Sci. Math. 136(2012), no. 5, 521–573. http://dx.doi.Org/10.1016/j.bulsci.2011.12.004 Google Scholar
[6] Dinghas, A., Über einen geometrischen Satz von Wulfffur die Gleichgewichtsform von Kristallen. Z. Kristallogr. Mineral. Petrogr. 105(1944), no. Abt. A, 304–314.Google Scholar
[7] Figalli, A., Maggi, E., and Pratelli, A., A mass transportation approach to quantitative isoperimetric inequalities. Invent. Math. 182(2010), no. 1,167–211.http://dx.doi.Org/10.1 OO7/sOO222-O10-0261-z Google Scholar
[8] Fusco, N., Millot, V., and Morini, M., A quantitative isoperimetric inequality for fractional perimeters. J. Funct. Anal. 261(2011), no. 3, 697–715.http://dx.doi.0rg/IO.IOI6/j.jfa.2O11.02.012 Google Scholar
[9] Hou, S., Xiao, J., and Ye, D., A mixed volume from the anisotropic Riesz-potential. preprint.Google Scholar
[10] Hurri-Syrjänen, R. and Vähäkangas, A.V., Characterizations to the fractional Sobolev inequality arxiv:1312.3135. Google Scholar
[11] Ludwig, M., Anisotropic fractional Sobolev norms. Adv. Math. 252(2014), 150–157.http://dx.doi.Org/10.1016/j.aim.2013.10.024 Google Scholar
[12] Ludwig, M., Anisotropic fractional perimeters,. J. Differential Geom. 96(2014), no. 1, 77–93.Google Scholar
[13] Maz'ya, V., Sobolev spaces with applications to elliptic partial differential equations. Second edition, revised and augmented. Grundlehren der Mathematischen Wissenschaften 342, Springer, Heidelberg, 2011.Google Scholar
[14] Maz'ya, V. and Shaposhnikova, T., On the Bourgain, Brezis, and Mironescu theorem concerning limiting embeddings of fractional Sobolev spaces. J. Funct. Anal. 195(2002), no. 2, 230–238.http://dx.doi.org/10.1006/jfan.2002.3955 Google Scholar
[15] Maz'ya, V., Erratum to: “On the Bourgain, Brezis, and Mironescu theorem concerning limiting embeddings of fractional Sobolev spaces”. [J. Funct. Anal. 195 (2002) 230-238].J. Funct. Anal. 201(2003), 298–300.http://dx.doi.Org/10.1OO6/jfan.2OO2.3955 Google Scholar
[16] Silvestre, P., Capacities and embeddings via symmetrization and conductor inequalities. Proc. Amer. Math. Soc. 142(2014), no. 2, 497–505.http://dx.doi.org/10.1090/S0002-9939-2013-11778-8 Google Scholar
[17] Visintin, A., Nonconvex functionals related to multiphase systems. SIAM J. Math. Anal. 21(1990), 1281–1304.http://dx.doi.org/10.1137/0521071 Google Scholar
[18] Xiao, J., Homogeneous endpoint Besov space embeddings by Hausdorff capacity and heat equation. Adv. Math. 207(2006), no. 2, 828–846.http://dx.doi.Org/10.1016/j.aim.2006.01.010 Google Scholar
[19] Xiao, J., The sharp Sobolev and isoperimetric inequalities split twice. Adv. Math. 211(2007), 417–435.http://dx.doi.Org/10.1016/j.aim.2006.08.006 Google Scholar
[20] Xiao, J., Corrigendum to “The sharp Sobolev and isoperimetric inequalities split twice” [Adv. Math. 211 (2007) 417–435] Adv. Math. (2014).http://dx.doi.Org/10.1016/j.aim.2014.04.011 Google Scholar
[21] Xiao, J., The p-Faber-Krahn inequality noted. In: Around the research of Vladimir Maz'ya I. function spaces. Springer, New York, 2010, pp. 373–390.Google Scholar
[22] Xiao, J. , Optimal geometric estimates for fractional Sobolev capacities. C. R. Math. Acad. Sci. Paris, 354(2016), no. 2, 149–153.http://dx.doi.Org/10.1016/j.crma.2015.10.014 Google Scholar