Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-13T08:16:46.756Z Has data issue: false hasContentIssue false
  • English
  • Français

The Analytic Character of the Birkhoff Interpolation Polynomials

Published online by Cambridge University Press:  20 November 2018

G. G. Lorentz
G. G. Lorentz*
Affiliation:
The University of Texas at Austin, Austin, Texas
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let E be an m × (n + 1) regular interpolation matrix with elements ei, k = (E)i, k which are zero or one, with n + 1 ones. Then for each f ∈ Cn[a, b] and each set of knots X: a ≦ x1 < … < xm ≦ b, there is a unique interpolation polynomial P(f, E, X; t) of degree ≦ n which satisfies

1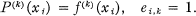

A recent paper [1] discussed the continuity of P, as a function of x1, …,xm(with coalescences allowed). We would like to study in this note the analytic character of P as a function of real or complex knots X: x1, …, xm. This is easy for the Lagrange or the Hermite interpolation. In this case P is a polynomial in x1, …, xm if f is a polynomial, and an entire function in x1, …, xm if f is entire.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 3 , 01 June 1982 , pp. 765 - 768
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Dyn, N., Lorentz, G. G. and Riemenschneider, S. D., Continuity of the Birkhoff interpolation, in print in SIAM J. Numer. Analysis.Google Scholar
2. Ferguson, D., The question of uniqueness for G. D. Birkhoff interpolation problem, J. Approx. Theory 2 (1969), 1–28.Google Scholar
3. Lorentz, G. G., Birkhoff interpolation problem, CNA report 103, The University of Texas in Austin (1975).Google Scholar
4. Lorentz, G. G., Independent sets of knots and singularity of interpolation matrices, J. Approx. Theory 30 (1980), 208–225.Google Scholar
5. Lorentz, G. G. and Riemenschneider, S. D., Recent progress in Birkhoff interpolation, in: Approximation theory and functional analysis (North-Holland Publ. Co., 1979, 187–236.Google Scholar
6. Lorentz, G. G. and Riemenschneider, S. D., Birkhoff interpolation: Some applications of coalescence, in : Quantitative approximation (Academic Press, New York), 1980–197.Google Scholar
7. Lorentz, G. G. and Zeller, K. L., Birkhoff interpolation problem: coalescence of rows, Arch. Math. 26 (1975), 189–192.Google Scholar