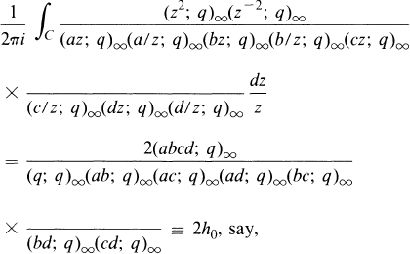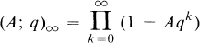Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Rahman, Mizan
1986.
Another Conjectured q-Selberg Integral.
SIAM Journal on Mathematical Analysis,
Vol. 17,
Issue. 5,
p.
1267.
Rahman, Mizan
1988.
A projection formula for the Askey-Wilson polynomials and an application.
Proceedings of the American Mathematical Society,
Vol. 103,
Issue. 4,
p.
1099.
Rahman, Mizan
1988.
Some Extensions of Askey-Wilson's Q-Beta Integral and the Corresponding Orthogonal Systems.
Canadian Mathematical Bulletin,
Vol. 31,
Issue. 4,
p.
467.
Wilson, James A.
1991.
Orthogonal Functions from Gram Determinants.
SIAM Journal on Mathematical Analysis,
Vol. 22,
Issue. 4,
p.
1147.
Rahman, Mizan
1991.
Biorthogonality of a System of Rational Functions with Respect to a Positive Measure on $[ - 1,1]$.
SIAM Journal on Mathematical Analysis,
Vol. 22,
Issue. 5,
p.
1430.
Atakishiyev, N. M.
and
Suslov, S. K.
1992.
Progress in Approximation Theory.
Vol. 19,
Issue. ,
p.
1.
Gustafson, Robert A.
1992.
Some q-Beta and Mellin–Barnes Integrals with Many Parameters Associated to the Classical Groups.
SIAM Journal on Mathematical Analysis,
Vol. 23,
Issue. 2,
p.
525.
Denis, R. Y.
and
Gustafson, R. A.
1992.
An $SU(n)$q-Beta Integral Transformation and Multiple Hypergeometric Series Identities.
SIAM Journal on Mathematical Analysis,
Vol. 23,
Issue. 2,
p.
552.
Rahman, Mizan
and
Suslov, S. K.
1993.
Methods of Approximation Theory in Complex Analysis and Mathematical Physics.
Vol. 1550,
Issue. ,
p.
131.
Askey, R.
and
Suslov, S. K.
1993.
Theq-harmonic oscillator and the Al-Salam and Carlitz polynomials.
Letters in Mathematical Physics,
Vol. 29,
Issue. 2,
p.
123.
Gustafson, Robert A.
1994.
Some q-Beta Integrals on $SU(n)$ and $Sp(n)$ That Generalize the Askey–Wilson and Nasrallah–Rahman Integrals.
SIAM Journal on Mathematical Analysis,
Vol. 25,
Issue. 2,
p.
441.
Al-Salam, Waleed A.
and
Ismail, Mourad E. H.
1994.
A 𝑞-beta integral on the unit circle and some biorthogonal rational functions.
Proceedings of the American Mathematical Society,
Vol. 121,
Issue. 2,
p.
553.
Ismail, M. E. H.
and
Masson, D. R.
1994.
𝑞-Hermite polynomials, biorthogonal rational functions, and 𝑞-beta integrals.
Transactions of the American Mathematical Society,
Vol. 346,
Issue. 1,
p.
63.
Rahman, Mizan
and
Suslov, Sergei K.
1994.
The Pearson Equation and the Beta Integrals.
SIAM Journal on Mathematical Analysis,
Vol. 25,
Issue. 2,
p.
646.
Спиридонов, Вячеслав Павлович
and
Spiridonov, Vyacheslav Pavlovich
2001.
Об эллиптической бета-функции.
Успехи математических наук,
Vol. 56,
Issue. 1,
p.
181.
Spiridonov, V. P.
and
Zhedanov, A. S.
2001.
Special Functions 2000: Current Perspective and Future Directions.
p.
365.
Spiridonov, V. P.
2001.
Integrable Structures of Exactly Solvable Two-Dimensional Models of Quantum Field Theory.
p.
305.
Spiridonov, V P
2001.
On the elliptic beta function.
Russian Mathematical Surveys,
Vol. 56,
Issue. 1,
p.
185.
Неретин, Юрий Александрович
and
Neretin, Yurii Aleksandrovich
2002.
Бета-интегралы и конечные ортогональные системы многочленов Вильсона.
Математический сборник,
Vol. 193,
Issue. 7,
p.
131.
van Diejen, J.F.
and
Spiridonov, V.P.
2002.
Elliptic Beta Integrals and Mudular Hypergeometric Sums: An Overview.
Rocky Mountain Journal of Mathematics,
Vol. 32,
Issue. 2,