Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-06T06:15:57.304Z Has data issue: false hasContentIssue false
  • English
  • Français

An Inequality Concerning Analytic Functions with a Positive Real Part

Published online by Cambridge University Press:  20 November 2018

Thomas H. MacGregor
Thomas H. MacGregor*
Affiliation:
State University of New York at Albany, Albany, New York
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

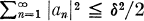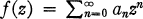This paper contains an inequality about functions which are analytic and have a positive real part in the unit disk. A first consequence of the inequality is the fact that if is analytic for |z| < 1 and has values lying in a strip of width δ. This result is known and was first proved by Tammi (1).

Our second theorem is a generalization of this. Namely, if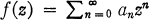is analytic for |z| < 1 and satisfies Re{zmf(m>(z)} ≧ A and

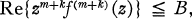
then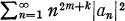converges.

Another application of our fundamental inequality is the following. Let 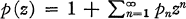be analytic for |z| < 1 and satisfy Re p(z) ≧ 0 and set 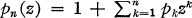and .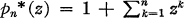

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 1172 - 1177
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Tammi, O., Note on Gutzmer's coefficient theorem, Rev. Fac. Sci. Univ. Istanbul Sér. A 22 (1957), 9–12.Google Scholar