Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T20:01:27.978Z Has data issue: false hasContentIssue false
  • English
  • Français

An Improved Subgroup Theorem for HNN Groups with Some Applications

Published online by Cambridge University Press:  20 November 2018

A. Karrass ,
A. Pietrowski  and
D. Solitar
A. Karrass
Affiliation:
York University, Downsview, Ontario
A. Pietrowski
Affiliation:
University of Toronto, Toronto, Ontario
D. Solitar
Affiliation:
York University, Downsview, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [4], a subgroup theorem for HNN groups was established. The theorem was proved by embedding the given HNN group in a free product with amalgamated subgroup and then applying the subgroup theorem of [3]. In this paper we obtain a sharper form of the subgroup theorem of [4] by applying the Reidemeister-Schreier method directly, using an appropriate Schreier system of coset representatives. Specifically, we prove (in Theorem 1) that if H is a subgroup of the HNN group

1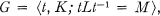

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 1 , February 1974 , pp. 214 - 224
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Cohen, D. E., Subgroups of HNN groups (to appear in J. Austral. Math. Soc, Hanna Neumann memorial issue).Google Scholar
2. Karrass, A., Pietrowski, A., and Solitar, D., Finite and infinite cyclic extensions of free groups (to appear in J. Austral. Math. Soc, Hanna Neumann memorial issue).Google Scholar
3. Karrass, A. and Solitar, D., The subgroups of a free product of two groups with an amalgamated subgroup, Trans. Amer. Math. Soc. 149 (1970), 227–255.Google Scholar
4. Karrass, A. and Solitar, D., Subgroups of HNN groups and groups with one defining relation, Can. J. Math. 28 (1971), 627–643.Google Scholar
5. Karrass, A. and Solitar, D., The free product of two groups with a malnormal amalgamated subgroup, Can. J. Math. 23 (1971), 933–959.Google Scholar
6. Karrass, A. and Solitar, D., On the presentation of Kleinian function groups (to appear).Google Scholar
7. Magnus, W., Karrass, A., and Solitar, D., Combinatorial group theory, Pure and Appl. Math., Vol. 18 (Interscience, New York, 1966).Google Scholar
8. Mahimovski, V. L., Directly decomposable groups with one defining relation, Ivanov. Gos. Ped. Inst. Ucen. Zap. 106 (1971), 115–122.Google Scholar
9. Moldavanski, D. I., Certain subgroups of groups with one defining relation, Sibirsk. Mat. Ž. 8 (1967), 1370–1384.Google Scholar
10. Murasugi, K., The center of the group of a link, Proc. Amer. Math. Soc. 16 (1965), 1052–1056.Google Scholar
11. Newman, B. B., Some results on one-relator groups, Bull. Amer. Math. Soc. 74 (1968), 568–571.Google Scholar
12. Pietrowski, A., The isomorphism problem for one-relator groups having non-trivial center (to appear).Google Scholar
13. Stallings, J., Groups of cohomological dimension one, Proc. Sympos. Pure Math., Vol. 17 (Amer. Math. Soc, Providence R.I., 1970), 124-128.Google Scholar
14. Stallings, J., Characterization of tree products of finitely many groups (to appear).Google Scholar
15. Wall, C. T. C., Rational Ruler characteristics, Proc. Cambridge Philos. Soc. 57 (1961), 182–184.Google Scholar