Published online by Cambridge University Press: 20 November 2018
The main object of this paper is to prove the following:
Theorem. Let f1, … ,fk be linearly independent continuous functions on a compact space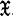 . Then for 1 ≤ s ≤ k there exist real numbers aij, 1 ≤ i ≤ s, 1 ≤ j ≤ k, with {aij, 1 ≤ i, j ≤ s} n-singular, and a discrete probability measure ε*on
. Then for 1 ≤ s ≤ k there exist real numbers aij, 1 ≤ i ≤ s, 1 ≤ j ≤ k, with {aij, 1 ≤ i, j ≤ s} n-singular, and a discrete probability measure ε*on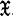 , such that
, such that
(a) the functions gi = Σj=1kaijfj 1 ≤ i ≤ s, are orthonormal (ε*) to the fj for s < j ≤ k;
(b)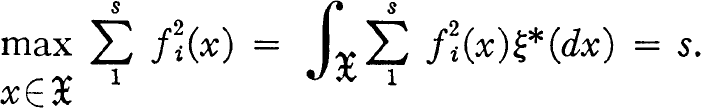
The result in the case s = k was first proved in (2). The result when s < k, which because of the orthogonality condition of (a) is more general than that when s = k, was proved in (1) under a restriction which will be discussed in § 3. The present proof does not require this ad hoc restriction, and is more direct in approach than the method of (2) (although involving as much technical detail as the latter in the case when the latter applies).