Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-25T01:22:39.905Z Has data issue: false hasContentIssue false
  • English
  • Français

An Extension of Meyer's Theorem on Indefinite Ternary Quadratic Forms

Published online by Cambridge University Press:  20 November 2018

Burton W. Jones
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let f be a ternary quadratic form whose matrix F has integral elements with g.c.d. 1, that is, an improperly or properly primitive form according as all diagonal elements are even or not. Let d be the determinant of f (denoted by 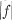) Ω, the g.c.d. of the 2-rowed minors of F. Then d = Ω2 Δ determines an integer Δ. Two forms f in the same genus have the same invariants Ω, Δ, d. The form whose matrix is adj F/Ω, is called the reciprocal form of f.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 4 , 1952 , pp. 120 - 128
Copyright
Copyright © Canadian Mathematical Society 1952

References

1. Dickson, L. E., Studies in the theory of numbers (Chicago, 1930).Google Scholar
2. Jones, B. W., The arithmetic theory of quadratic forms (Tenth Carus Monograph, Math. Assoc. Amer., 1950).Google Scholar
3. Meyer, A., Über indefinite ternare quadratische Formen, J. Reine Angew. Math., vol. 116 (1896), 317–325.Google Scholar