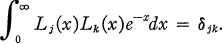Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T08:53:24.845Z Has data issue: false hasContentIssue false
  • English
  • Français

An Alternative Approach to Laguerre Polynomial Identities in Combinatorics

Published online by Cambridge University Press:  20 November 2018

Wayne W. Barrett
Wayne W. Barrett*
Affiliation:
Texas A and M University, College Station, Texas
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. In their paper “Permutation Problems and Special Functions,” Askey and Ismail [1] give the following striking identity. Consider three boxes containing j, k, m distinguishable balls, and consider all possible rearrangements of these balls such that each box still has the same number of balls; i.e., j end up in the first, k in the second, m in the third. One disregards the order of the balls within a box so there are (j + k + m)!/(j!k!m!) possible rearrangements. Let RE be the number of rearrangements where an even number of balls change boxes and R0 the number of rearrangements where an odd number change boxes. The identity is

(1.1)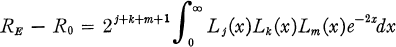

where

(1.2)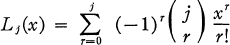

is the jth Laguerre polynomial. These polynomials are orthonormal with respect to the weight function e–x; i.e.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 2 , 01 April 1979 , pp. 312 - 319
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Askey, R. and Ismail, M. E. H., Permutation problems and special functions, Can. J. Math. 28 (1976), 853–874.Google Scholar
2. Askey, R., Ismail, M. E. H. and Koornwinder, T., Weighted permutation problems and Laguerre polynomials, J. Comb. Theory, ser. A, (1978), (to appear).Google Scholar
3. Askey, R., Ismail, M. E. H. and Rashed, T., A derangement problem, MRC Technical Summary Report #1522 (1975).Google Scholar
4. Feller, W., An introduction to probability theory and its applications, Volume I, Third Edition (John Wiley & Sons, Inc., New York, 1968).Google Scholar
5. Ismail, M. E. H. and Tamhankar, M. V., A combinatorial approach to positivity problems, Applied Mathematics Technical Report 77-AM-4, McMaster University (1977).Google Scholar
6. Jackson, D. M., Laguerre polynomials and derangements, Math. Proc. of the Camb. Phil. Soc. 80 (1976), 213–214.Google Scholar
7. Koornwinder, T., Positivity proofs for linearization and connection coefficients of orthogonal polynomials satisfying an addition theorem, (to appear).Google Scholar
8. MacMahon, P. A., Combinatory analysis, Volume I (Chelsea, New York, 1960).Google Scholar