No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
We produce ample (resp. NEF, eventually free) divisors in the Kontsevich space
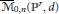 ${{\overline{\mathcal{M}}}_{\text{0,}n}}\left( {{\mathbb{P}}^{r}},d \right)$
of
${{\overline{\mathcal{M}}}_{\text{0,}n}}\left( {{\mathbb{P}}^{r}},d \right)$
of  $n$-pointed, genus 0, stable maps to
$n$-pointed, genus 0, stable maps to 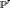 ${{\mathbb{P}}^{r}}$, given such divisors in
${{\mathbb{P}}^{r}}$, given such divisors in
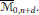 ${{\overline{\mathcal{M}}}_{\text{0,}n+d}}$ We prove that this produces all ample (resp. NEF, eventually free) divisors in
${{\overline{\mathcal{M}}}_{\text{0,}n+d}}$ We prove that this produces all ample (resp. NEF, eventually free) divisors in 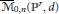 ${{\overline{\mathcal{M}}}_{\text{0,}n}}\left( {{\mathbb{P}}^{r}},\,d \right)$ As a consequence, we construct a contraction of the boundary
${{\overline{\mathcal{M}}}_{\text{0,}n}}\left( {{\mathbb{P}}^{r}},\,d \right)$ As a consequence, we construct a contraction of the boundary 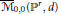 $\,\,\mathop{\bigcup }_{k=1}^{\left\lfloor {d}/{2}\; \right\rfloor }\,{{\Delta }_{k,d-k}}$ in
$\,\,\mathop{\bigcup }_{k=1}^{\left\lfloor {d}/{2}\; \right\rfloor }\,{{\Delta }_{k,d-k}}$ in 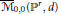 ${{\overline{\mathcal{M}}}_{\text{0,}0}}\left( {{\mathbb{P}}^{r}},d \right)$
analogous to a contraction of the boundary
${{\overline{\mathcal{M}}}_{\text{0,}0}}\left( {{\mathbb{P}}^{r}},d \right)$
analogous to a contraction of the boundary 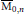 $\mathop{\bigcup }_{k=3}^{\left\lfloor {n}/{2}\; \right\rfloor }\,{{\widetilde{\Delta }}_{k,n-k}}$ in
$\mathop{\bigcup }_{k=3}^{\left\lfloor {n}/{2}\; \right\rfloor }\,{{\widetilde{\Delta }}_{k,n-k}}$ in 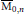 ${{\overline{\mathcal{M}}}_{\text{0,}n}}$ first constructed by Keel and McKernan.
${{\overline{\mathcal{M}}}_{\text{0,}n}}$ first constructed by Keel and McKernan.