Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T06:04:58.943Z Has data issue: false hasContentIssue false
  • English
  • Français

The Ample Cone for a K3 Surface

Published online by Cambridge University Press:  20 November 2018

Arthur Baragar
Arthur Baragar*
Affiliation:
Department of Mathematical Sciences, University of Nevada Las Vegas, Las Vegas, NV 89154-4020, U.S.A. email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we give several pictorial fractal representations of the ample or Kähler cone for surfaces in a certain class of 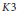$K3$ surfaces. The class includes surfaces described by smooth (2, 2, 2) forms in 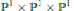${{\mathbb{P}}^{1}}\,\times \,{{\mathbb{P}}^{1}}\,\times \,{{\mathbb{P}}^{1}}$ defined over a sufficiently large number field 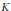$K$ that have a line parallel to one of the axes and have Picard number four. We relate the Hausdorff dimension of this fractal to the asymptotic growth of orbits of curves under the action of the surface's group of automorphisms. We experimentally estimate the Hausdorff dimension of the fractal to be 1.296 ± .010.

Keywords

14J2814J5011D4111D7211H5611G1037F3537D05FractalHausdorff dimensionK3 surfaceKleinian groupsdynamics
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 3 , 01 June 2011 , pp. 481 - 499
Copyright
Copyright © Canadian Mathematical Society 2011

References

[Ba1] Baragar, A., Orbits of curves on certain K3 surfaces. Compositio Math. 137(2003), no. 2, 115–134. doi:10.1023/A:1023960725003 Google Scholar
[Ba2] Baragar, A., Rational points on K3 surfaces in P1 × P1 × P1. Math. Ann. 305(1996), no. 3, 541–558. doi:10.1007/BF01444236 Google Scholar
[Ba3] Baragar, A., Fractals and eigenvalue of the Laplacian on certain noncompact surfaces. Experiment. Math. 15(2006), no. 1, 33–42.Google Scholar
[B-L] Baragar, A. and van Luijk, R. , K3 surfaces with Picard number three and canonical heights. Math. Comp. 76(2007), no. 259, 1493–1498. doi:10.1090/S0025-5718-07-01962-X Google Scholar
[B-McK] Baragar, A. and McKinnon, D., K3 surfaces, rational curves, and rational points. J. Number Theory 130(2010), no. 7, 1470–1479. doi:10.1016/j.jnt.2010.02.014 Google Scholar
[Bi] Billard, H., Propriétés arithmétiques d’une famille de surfaces K3. Compositio Math. 108(1997), no. 3, 247–275. doi:10.1023/A:1000128300511 Google Scholar
[C] Cantat, S., Dynamique des automorphismes des surfaces K3. Acta Math. 187(2001), no. 1, 1–57. doi:10.1007/BF02392831 Google Scholar
[L-M-W] Lagarias, J. C., Mallows, C. L., and A. R.Wilks, Beyond the Descartes circle theorem. Amer. Math. Monthly 109(2002), no. 4, 338–361. doi:10.2307/2695498 Google Scholar
[K-K] Keum, J. and Kondo, S., The automorphism groups of Kummer surfaces associated with the product of two elliptic curves. Trans. Amer. Math. Soc. 353(2001), no. 4, 1469–1487. doi:10.1090/S0002-9947-00-02631-3 Google Scholar
[Kon] Kondo, S., The automorphism group of a generic Jacobian Kummer surface. J. Algebraic Geom. 7(1998), no. 3, 589–609.Google Scholar
[Kov] Kovács, S., The cone of curves of a K3 surface. Math. Ann. 300(1994), no. 4, 681–691. doi:10.1007/BF01450509 Google Scholar
[L-P] Lax, P. D. and Phillips, R. S., The asymptotic distribution of lattice points in Euclidean and non-Euclidean spaces. J. Funct. Anal. 46(1982), no. 3, 280–350. doi:10.1016/0022-1236(82)90050-7 Google Scholar
[McM] McMullen, C. T., Dynamics on K3 surfaces: Salem numbers and Siegel disks. J. Reine Angew. Math. 545(2002), 201–233.Google Scholar
[M-S-W] Mumford, D., Series, C., and Wright, D., Indra's pearls. The vision of Felix Klein. Cambridge University Press, New York, 2002.Google Scholar
[Mo] Morrison, D. R., On K3 surfaces with large Picard number. Invent. Math. 75(1984), no. 1, 105–121. doi:10.1007/BF01403093 Google Scholar
[N1] Nikulin, V. V., K3 surfaces with a finite number of automorphisms and a Picard group of rank three, Algebraic geometry and its applications. (Russian) Trudy Mat. Inst. Steklov. 165(1984), 119–142.Google Scholar
[N2] Nikulin, V. V., Quotient-groups of groups of automorphisms of hyperbolic forms of subgroups generated by 2-reflections. (Russian) Dokl. Akad. Nauk SSSR 248(1979), no. 6, 1307–1309.Google Scholar
[N3] Nikulin, V. V., Quotient-groups of groups of automorphisms of hyperbolic forms by subgroups generated by 2-reflections. Algebro-geometric applications. (Russian) In: Current problems in mathematics, 18, Akad. Nauk SSR, Vsesoyuz. Inst. Nauchn. i Tekhn. Informatsii, Moscow, 1981, pp. 3–114.Google Scholar
[P-S] Phillips, R. and Sarnak, P., The Laplacian for domains in hyperbolic space and limit sets of Kleinian groups. Acta. Math. 155(1985), no. 3–4, 173–241. doi:10.1007/BF02392542 Google Scholar
[PS-S] Pjateckii-Sapiro, I. I. and Safarevič, I. R., Torelli's theorem for algebraic surfaces of type K3. (Russian) Nauk SSSR Ser. Mat. 35(1971), 530–572.Google Scholar
[R] Ratcliff, J. S., Foundations of hyperbolic manifolds. Springer-Verlag, New York, 1994.Google Scholar
[St] Sterk, H.,Finiteness results for algebraic K3 surfaces. Math. Z. 189(1985), no. 4, 507–513. doi:10.1007/BF01168156 Google Scholar
[Su] Sullivan, D., Entropy, Hausdorff measures old and new, and limit sets of geometrically finite Kleinian groups. Acta Math. 153(1984), no. 3–4, 259–277. doi:10.1007/BF02392379 Google Scholar
[V] Vinberg, É. B., The two most algebraic K3 surfaces. Math. Ann. 265(1983), no. 1, 1–21. doi:10.1007/BF01456933 Google Scholar
[W] Wang, L., Rational points and canonical heights on K3-surfaces in P1 × P1 × P1. In: Recent developments in the inverse Galois problem (Seattle,WA, 1993), Contemp. Math., 186, American Mathematical Society, Providence, RI, 1995, pp. 273–289.Google Scholar