Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T01:38:57.447Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost Split Sequences whose Middle Term has at most Two Indecomposable Summands

Published online by Cambridge University Press:  20 November 2018

M. Auslander ,
R. Bautista ,
M. I. Platzeck ,
I. Reiten  and
S. O. Smalø
M. Auslander
Affiliation:
Brandeis University, Waltham, Massachusetts
R. Bautista
Affiliation:
University of Mexico, Mexico
M. I. Platzeck
Affiliation:
University of Bahiá Blanca, Argentina
I. Reiten
Affiliation:
University of Trondheim, Norway
S. O. Smalø
Affiliation:
University of Trondheim, Norway
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Λ be an artin algebra, and denote by mod Λ the category of finitely generated Λ-modules. All modules we consider are finitely generated.

We recall from [6] that a nonsplit exact sequence 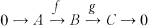in mod A is said to be almost split if A and C are indecomposable, and given a map h: X → C which is not an isomorphism and with X indecomposable, there is some t: X → B such that gt = h.

Almost split sequences have turned out to be useful in the study of representation theory of artin algebras. Given a nonprojective indecomposable Λ-module C (or an indecomposable noninjective Λ-module A), we know that

there exists a unique almost split sequence 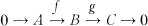[6, Proposition 4.3], [5, Section 3].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 5 , 01 October 1979 , pp. 942 - 960
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Auslander, M., Representation theory of artin algebras If Comm. in Algebra 1 (1974), 269–310.Google Scholar
2. Auslander, M., Applications of morphisms determined by modules, Representation theory of algebras (Proc. of the Philadelphia conf. 1976) Lecture Notes in Pure and Applied Math., Vol. 37 (M. Dekker, N.V., 1978).Google Scholar
3. Auslander, M. and Platzeck, M. I., Representation theory of hereditary artin algebras, Representation theory of algebras (Proc. of the Philadelphia conf. 1976) Lecture Notes in Pure and Applied Math., Vol. 37 (M. Dekker, N.Y., 1978).Google Scholar
4. Auslander, M. and Reiten, I., Stable equivalence of artin algebras, Proc. of the conf. on orders, groups rings and related topics, Ohio 1972, Springer Lecture Note. 353 (1973), 8–64.Google Scholar
5. Auslander, M. and Reiten, I., Stable equivalence of dualizing R-varieties, Adv. in Math. (1974), 300–366.Google Scholar
6. Auslander, M. and Reiten, I., Representation theory of artin algebras III, Comm. in Algebr. 3 (1975), 239–294.Google Scholar
7. Auslander, M. and Reiten, I., Representation theory of artin algebras IV, Comm. in Algebr. 5 (1977), 443–518.Google Scholar
8. Auslander, M. and Reiten, I., Representation theory of artin algebras V, Comm. in Algebr. 5 (1977), 519–554.Google Scholar
9. Auslander, M. and Reiten, I., Representation theory of artin algebras VI, Comm. in Algebra.Google Scholar
10. Dlab, V. and Ringel, C. M., Indecomposable representations of graphs and algebras, Memoirs Amer. Math. Soc. Vol. 6, No 173 (1976).Google Scholar
11. Harada, M. and Sai, V., On categories of indecomposable modules I, Osaka J. Math. 7 (1970), 323–344.Google Scholar
12. Muller, W., Unzerlegbare moduln iiber artinsehen ringen, Math. Z. 137 (1974), 197–220.Google Scholar
13. Ringel, C. M., Finite dimensional hereditary algebras of wild representation type, Math. Z. 161 (1978), 235–255.Google Scholar