Soit $k$ un corps de caractéristique $p$ quelconque. Nous définissons la catégorie des $k$-algèbres de cochaînes fortement quasi-commutatives et nous donnons une condition nécessaire et suffisante pour que l’algèbre de cohomologie à coefficients dans 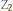${{\text{Z}}_{2}}$ d’un objet de cette catégorie soit un module instable sur l’algèbre de Steenrod à coefficients dans 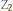${{\text{Z}}_{2}}$.

A tout c.w. complexe simplement connexe de type fini 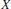$X$ on associe une $k$-algèbre de cochaînes fortement quasi-commutative; la structure de module sur l’algèbre de Steenrod définie sur l’algèbre de cohomologie de celle-ci coïncide avec celle de ${{H}^{*}}(X;\,{{\text{Z}}_{2}})$.

We define the category of strongly quasi-commutative cochain $k$-algebras, where $k$ is a field of any characteristic $p$. We give a necessary and sufficient condition which enables the cohomology algebra with 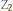${{\text{Z}}_{2}}$-coefficients of an object in this category to be an unstable module on the 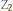${{\text{Z}}_{2}}$-Steenrod algebra.

To each simply connected c.w. complex of finite type 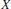$X$ is associated a strongly quasi-commutative model and the module structure over the 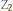${{\text{Z}}_{2}}$-Steenrod algebra defined on the cohomology of this model is the usual structure on ${{H}^{*}}(X;\,{{\text{Z}}_{2}})$.