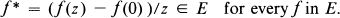Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T19:21:39.095Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebras of Bounded Analytic Functions containing the Disk Algebra

Published online by Cambridge University Press:  20 November 2018

Keiji Izuchi  and
Yuko Izuchi
Keiji Izuchi
Affiliation:
Kanagawa University, Yokohama, Japan
Yuko Izuchi
Affiliation:
Kanagawa Dental College, Yokosuka, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let D be the open unit disk and let ∂D be its boundary. We denote by C the algebra of continuous functions on ∂d, and by L∞ the algebra of essentially bounded measurable functions with respect to the normalized Lebesgue measure m on ∂D. Let H∞ be the algebra of bounded analytic functions on D. Identifying with their boundary functions, we regard H∞ as a closed subalgebra of L∞. Let A = H∞ Pi C, which is called the disk algebra. The algebras A and H∞ have been studied extensively [5, 6, 7]. In these fifteen years, norm closed subalgebras between H∞ and L∞, called Douglas algebras, have received considerable attention in connection with Toeplitz operators [12]. A norm closed subalgebra between A and H∞ is called an analytic subalgebra. In [2], Dawson studied analytic subalgebras and he remarked that there are many different types of analytic subalgebras. One problem is to study which analytic subalgebras are backward shift invariant. Here, a subset E of H∞ is called backward shift invariant if

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 1 , 01 February 1986 , pp. 87 - 108
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Chang, S. Y. and Marshall, D., Some algebras of bounded analytic functions containing the disk algebra, Lecture Notes in Math. 604, 12–20 (Springer-Verlag, Berlin Heidelberg, 1977).Google Scholar
2. Dawson, D., Subalgebras of H°°, Thesis, Univ. of Indiana (1975).Google Scholar
3. Fisher, S., Algebras of bounded functions invariant under the restricted backward shift, J. Funct. Anal. 12 (1973), 236–245.Google Scholar
4. Fisher, S., Invariant subalgebras of the backward shift, Amer. J. Math. 95 (1973), 537–552.Google Scholar
5. Gamelin, T., Uniform algebras (Prentice-Hall, Englewood Cliffs, N. J., 1969).Google Scholar
6. Garnett, J., Bounded analytic functions (Academic Press, New York, 1981).Google Scholar
7. Hoffman, K., Banach spaces of analytic functions (Prentice-Hall, Englewood Cliffs, N. J., 1962).Google Scholar
8. Muto, T. and Nakazi, T., Maximality theorems for some closed subalgebras between A and H∞, Arch. Math. 43 (1984), 173–178.Google Scholar
9. Nakazi, T., Algebras generated by z and an inner function, Arch. Math. 42 (1984), 545–548.Google Scholar
10. Nishizawa, K., On closed subalgebras between A and H∞ II, Tokyo J. Math. 5 (1982), 157–169.Google Scholar
11. Sarason, D., Algebras of functions on the unit circle, Bull. Amer. Math. Soc. 79 (1973), 286–299.Google Scholar
12. Sarason, D., Function theory on the unit circle, Lecture Note (Virginia Polytec. Inst, and State Univ., Virginia, 1978).Google Scholar
13. Stegenga, D., Sums of invariant subspaces, Pacific J. Math. 70 (1977), 567–584.Google Scholar
14. Wolff, T., Two algebras of bounded functions, Duke Math. J. 49 (1982), 321–328.Google Scholar