Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T00:55:04.131Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebras Intertwining Normal and Decomposable Operators

Published online by Cambridge University Press:  20 November 2018

Ali A. Jafarian
Ali A. Jafarian*
Affiliation:
Tehran University of Technology, Tehran, Iran
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The celebrated result of Lomonosov [6] on the existence of invariant subspaces for operators commuting with a compact operator have been generalized in different directions (for example see [2], [7], [8], [9]). The main result of [9] (see also [7]) is: If 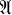is a norm closed algebra of (bounded) operators on an infinite dimensional (complex) Banach space 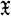, if K is a nonzero compact operator on 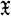, and if 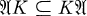then 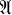has a non-trivial (closed) invariant subspace. In [7], it is mentioned that the above result holds if instead of compactness for K we assume that K is a non-invertible injective operator with a non-zero eigenvalue belonging to the class of decomposable, hyponormal, or subspectral operators.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 6 , 01 December 1979 , pp. 1339 - 1344
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Colojoara, I. and Foias, C., Theory of generalized spectral operators (Gordon and Breach, New York, 1968).Google Scholar
2. Daughtry, J., An invariant subspace theorem, Proc. Amer. Math. Soc. 49 (1975), 267–268.Google Scholar
3. Dunford, N. and Swchartz, J., Linear operators, Part III: Spectral Operators (New York, Interscience, 1971).Google Scholar
4. Foias, C., Invariant para-closed subspaces, Indiana Univ. Math. J. 21 (1972), 887–906.Google Scholar
5. Frunza, S., Spectral decomposition and duality, 111. J. Math. 20 (1976), 314–321.Google Scholar
6. Lomonosov, V., Invariant subspaces for the family of operators which commute with a completely continuous operator, Funct. Anal, and Appl. 7 (1973), 213–214.Google Scholar
7. Nordgren, E., Radjabalipour, M., Radjavi, H. and Rosenthal, P., Algebras intertwining compact operators, Acta Sci. Math. (Szeged),. 39 (1977), 115–119.Google Scholar
8. Pearcy, C. and Shields, A., A survey of the Lomonosov technique in the theory of invariant subspaces, Topics in Operator Theory, Math. Surveys 13, Amer. Math. Soc. Providence, (1974), 221–228.Google Scholar
9. Radjabalipour, M. and Radjavi, H., Compact operator ranges and transitive algebras, to appear in Bull. Lond. Math. Soc.Google Scholar