Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T01:03:49.013Z Has data issue: false hasContentIssue false
  • English
  • Français

Akcoglu's Ergodic Theorem for Uniform Sequences

Published online by Cambridge University Press:  20 November 2018

James H. Olsen
James H. Olsen*
Affiliation:
North Dakota State University, Fargo, North Dakota
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (X, F,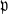) be a sigma-finite measure space. In what follows we assume p fixed, 1 < p < ∞ . Let T be a contraction of Lp(X, F, μ) (‖T‖,p ≦ 1). If ƒ ≧ 0 implies Tƒ ≧ 0 we will say that T is positive. In this paper we prove that if 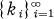is a uniform sequence (see Section 2 for definition) and T is a positive contraction of Lp, then

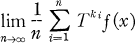
exists and is finite almost everywhere for every ƒ ∊ Lp(X, F, μ).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 4 , April 1980 , pp. 880 - 884
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Akcoglu, M. A., A. pointwise ergodic theorem in Lp-spaces, Can. J. Math. 27 (1975), 1075–1082.Google Scholar
2. Brunei, A. and Keene, M., Ergodic theorems for operator sequences, Z. Wahrscheinlichkeitstheorie verw. Geb. 12 (1969), 231–240.Google Scholar
3. Lorch, R. L., Spectral theory (Oxford, 1962).Google Scholar
4. Sato, R., On the individual ergodic theorem for subsequences, Studia Mathematica. TXL. V. (1973), 31–35.Google Scholar