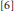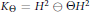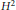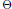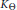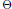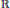This paper is a continuation of $[6]$. We consider the model subspaces ${{K}_{\Theta }}={{H}^{2}}\ominus \Theta {{H}^{2}}$ of the Hardy space ${{H}^{2}}$ generated by an inner function $\Theta $ in the upper half plane. Our main object is the class of admissible majorants for ${{K}_{\Theta }}$, denoted by Adm $\Theta $ and consisting of all functions $\omega $ defined on $\mathbb{R}$ such that there exists an 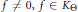$f\ne 0,f\in {{K}_{\Theta }}$ satisfying 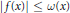$|f\left( x \right)|\,\le \,\omega \left( x \right)$ almost everywhere on 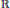$\mathbb{R}$. Firstly, using some simple Hilbert transform techniques, we obtain a general multiplier theorem applicable to any 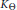${{K}_{\Theta }}$ generated by a meromorphic inner function. In contrast with 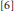$[6]$, we consider the generating functions 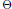$\Theta $ such that the unit vector 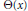$\Theta \left( x \right)$ winds up fast as $x$ grows from 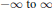$-\infty \,\text{to}\,\infty $. In particular, we consider 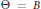$\Theta \,=\,B$ where $B$ is a Blaschke product with “horizontal” zeros, i.e., almost uniformly distributed in a strip parallel to and separated from 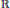$\mathbb{R}$. It is shown, among other things, that for any such 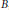$B$, any even $\omega $ decreasing on 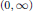$\left( 0,\,\infty \right)$ with a finite logarithmic integral is in Adm 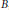$B$ (unlike the “vertical” case treated in 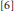$[6]$), thus generalizing (with a new proof) a classical result related to Adm 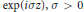$\exp \left( i\sigma z \right),\,\sigma \,>\,0$. Some oscillating $\omega $'s in Adm 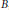$B$ are also described. Our theme is related to the Beurling-Malliavin multiplier theorem devoted to Adm 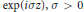$\exp \left( i\sigma z \right),\,\sigma \,>\,0$, and to de Branges’ space 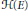$H\left( E \right)$.