Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-29T15:24:58.027Z Has data issue: false hasContentIssue false
  • English
  • Français

Admissible Majorants for Model Subspaces of H2, Part I: Slow Winding of the Generating Inner Function

Published online by Cambridge University Press:  20 November 2018

Victor Havin  and
Javad Mashreghi
Victor Havin
Affiliation:
Department of Mathematics and Statistics, McGill University, Montreal, Quebec, H3A 2K6 e-mail: [email protected] Department of Mathematics and Mechanics, St. Petersburg State University, Russia 198904
Javad Mashreghi
Affiliation:
Département de mathématiques et de statistique, Université Laval, Laval, Québec, G1K 7P4 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

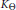A model subspace ${{K}_{\Theta }}$ of the Hardy space 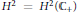${{H}^{2}}={{H}^{2}}\left( {{\mathbb{C}}_{+}} \right)$ for the upper half plane 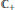${{\mathbb{C}}_{+}}$ is 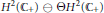${{H}^{2}}\left( {{\mathbb{C}}_{+}} \right)\ominus \Theta {{H}^{2}}\left( {{\mathbb{C}}_{+}} \right)$ where 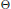$\Theta $ is an inner function in 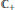${{\mathbb{C}}_{+}}$. A function 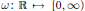$\omega :\,\mathbb{R}\mapsto [0,\,\infty )$ is called an admissible majorant for 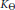${{K}_{\Theta }}$ if there exists an 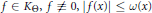$f\,\in \,{{K}_{\Theta }},\,f\,\not{\equiv }\,0,\,|f\left( x \right)|\,\le \,\omega \left( x \right)$ almost everywhere on 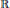$\mathbb{R}$. For some (mainly meromorphic) 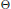$\Theta $'s some parts of Adm 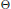$\Theta $ (the set of all admissible majorants for 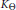${{K}_{\Theta }}$) are explicitly described. These descriptions depend on the rate of growth of arg 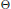$\Theta $ along 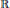$\mathbb{R}$. This paper is about slowly growing arguments (slower than $x$). Our results exhibit the dependence of Adm 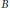$B$ on the geometry of the zeros of the Blaschke product 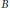$B$. A complete description of Adm 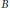$B$ is obtained for 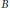$B$'s with purely imaginary (“vertical”) zeros. We show that in this case a unique minimal admissible majorant exists.

Keywords

30D5547A15Hardy spaceinner functionshift operatormodel subspaceHilbert transformadmissible majorant
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 6 , 01 December 2003 , pp. 1231 - 1263
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Ahern, P. and Clark, D., On Functions Orthogonal to Invariant Subspaces. Acta Math. 124(1970), 191–204.Google Scholar
[2] Alexandrov, A., Invariant subspaces of the backward shift operator in the space Hp p ∈ (0; 1). Investigations on linear operators and the theory of functions, IX, Zap. Nauchn. Sem. Leningrad Otdel. Mat. Inst. Steklov (LOMI) 92(1979), 7–29.Google Scholar
[3] Boas, R., Entire Functions. Academic Press, 1954.Google Scholar
[4] Beurling, A., On two problems concerning linear transformations in Hilbert space. Acta Math. 81(1949), 239–255.Google Scholar
[5] Beurling, A. and Malliavin, P., On Fourier transforms of measures with compact support. Acta Math. 107(1962), 291–309.Google Scholar
[6] de Branges, L., Hilbert Spaces of Entire Functions. Prentice Hall, 1968.Google Scholar
[7] de Branges, L., Some Hilbert spaces of entire functions. Trans. Amer. Math. Soc. 96(1960), 259–295.Google Scholar
[8] Cima, J. and Ross, W., The Backward Shift on the Hardy Space. Math. SurveysMonogr. 79, Amer. Math. Soc., 2000.Google Scholar
[9] Cohn, W., Unitary equivalence of restricted shifts. J. Operator Theory (1) 5(1981), 17–28.Google Scholar
[10] Conway, J., Functions of One Complex Variable. Second Edition, Springer Verlag, 1978.Google Scholar
[11] Douglas, R., Shapiro, H. and Shields, A., Cyclic vectors and invariant subspaces for backward shift operator. Ann. Inst. Fourier (Grenoble) 20(1970), 37–76.Google Scholar
[12] Duren, P., Theory of Hp Spaces. Academic Press, 1970.Google Scholar
[13] Dyakonov, K., On the moduli and arguments of analytic functions of Hp that are invariant for the backward shift operator. Sibirsk. Mat. Zh. 31(1990), 64–79.Google Scholar
[14] Garnett, J., Bounded Analytic Functions. Academic Press, 1981.Google Scholar
[15] Halmos, P., Introduction to Hilbert Space and the Theory of Spectral Multiplicity. Second Edition, Chelsea Publishing Company, 1957.Google Scholar
[16] Halmos, P., A Hilbert Space Problem Book. Second Edition, Springer Verlag, 1982.Google Scholar
[17] Havin, V. and Jöricke, B., The Uncertainty Principle in Harmonic Analysis. Springer-Verlag, 1994.Google Scholar
[18] Havin, V. and Mashreghi, Javad, Admissible majorants for model subspaces of H 2 , Part II: fast winding of the generating inner function. Canad. J. Math. 55(2003), 1264–1301.Google Scholar
[19] Helson, H., Lectures on Invariant Subspaces. Academic Press, 1964.Google Scholar
[20] Koosis, P., A relation between two results about entire functions of exponential type. Mat. Fiz. Anal. Geom. 5(1995), 212–231.Google Scholar
[21] Koosis, P., A result on polynomials and its relation to another, concerning entire functions of exponential type. Mat. Fiz. Anal. Geom. 5(1998), 68–86.Google Scholar
[22] Koosis, P., Introduction to Hp Spaces. Second Edition, Cambridge Tracts in Math. 115, 1998.Google Scholar
[23] Koosis, P., The Logarithmic Integral I. Cambridge Stud. Adv. Math. 12, 1988.Google Scholar
[24] Koosis, P., The Logarithmic Integral II. Cambridge Stud. Adv. Math. 21, 1992.Google Scholar
[25] Koosis, P., Leçons sur le Théorème de Beurling et Malliavin. Les Publications CRM, Montr éal, 1996.Google Scholar
[26] Levin, B., Distribution of zeros of Entire Functions. Transl. Math. Monogr. 5, 1980, Amer. Math. Soc.Google Scholar
[27] Neuwirth, J. and Newman, D., Positive H1/2 functions are constant. Proc. Amer. Math. Soc. (5) 18(1967), 9–8.Google Scholar
[28] Nagy, B. and Foiaş, C., Harmonic Analysis of Operators on Hilbert Space. North-Holland, 1970.Google Scholar
[29] Nikolski, N., Treatise on the Shift Operator. Springer 1986.Google Scholar
[30] Privalov, I., Intégral de Cauchy. Bulletin de l'Universit é Saratov, 1918.Google Scholar
[31] Titchmarsh, E., Introduction to the Theory of Fourier Integrals. Chelsea Publishing Company, 1962.Google Scholar
[32] Volberg, A., Thin and thick families of rational functions. Lecture Notes in Math. 864(1981), 440–480.Google Scholar
[33] Volberg, A. and Treil, S., Embedding theorems for invariant subspaces of the inverse shift operator. J. Soviet Math. (2) 42(1988), 1562–1572.Google Scholar
[34] Woracek, H., de Branges spaces of entire functions closed under forming difference quotients. Integral Equations Operator Theory (2) 37(2000), 238–249.Google Scholar
[35] Zygmund, A., Trigonometric Series. Vol I, Cambridge University Press, 1968.Google Scholar