Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T14:52:25.219Z Has data issue: false hasContentIssue false
  • English
  • Français

Adjacency Preserving Maps on Hermitian Matrices

Published online by Cambridge University Press:  20 November 2018

Wen-ling Huang  and
Peter Šemrl
Wen-ling Huang
Affiliation:
Fachbereich Mathematik, Schwerpunkt GD, Universität Hamburg, D-20146 Hamburg, Germany e-mail:[email protected]
Peter Šemrl
Affiliation:
Department of Mathematics, University of Ljubljana, SI-1000 Ljubljana, Slovenia e-mail:[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

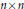Hua’s fundamental theorem of the geometry of hermitian matrices characterizes bijective maps on the space of all $n\times n$ hermitianmatrices preserving adjacency in both directions. The problem of possible improvements has been open for a while. There are three natural problems here. Do we need the bijectivity assumption? Can we replace the assumption of preserving adjacency in both directions by the weaker assumption of preserving adjacency in one direction only? Can we obtain such a characterization formaps acting between the spaces of hermitian matrices of different sizes? We answer all three questions for the complex hermitian matrices, thus obtaining the optimal structural result for adjacency preserving maps on hermitian matrices over the complex field.

Keywords

15A0315A0415A5715A99rankadjacency preserving maphermitian matrixgeometry of matrices
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 5 , October 2008 , pp. 1050 - 1066
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Alexandrov, A. D., Seminar report. Uspehi Mat. Nauk 37(1950), no. 3, 187.Google Scholar
[2] Alexandrov, A. D., On the axioms of relativity theory. Vestnik Leningrad Univ. Math. 19(1976), 5–28.Google Scholar
[3] Chow, W.-L., On the geometry of algebraic homogeneous spaces. Ann. of Math. 50(1949), 32–67.Google Scholar
[4] Fulton, W., Algebraic Topology: A First Course. Graduate Texts in Mathematics 153, Springer, New York, 1995.Google Scholar
[5] Hua, L. K., Geometries of matrices. I. Generalizations of von Staudt's theorem. Trans. Amer. Math. Soc. 57(1945), 441–481.Google Scholar
[6] Hua, L. K., Geometries of matrices I1. Arithmetical construction. Trans. Amer. Math. Soc. 57(1945), 482–490.Google Scholar
[7] Hua, L. K., Starting with the Unit Circle. Springer-Verlag, New York, 1981.Google Scholar
[8] Huang, W.-l., Höfer, R., and Wan, Z.-X., Adjacency preserving mappings of symmetric and Hermitian matrices. Aequationes Math. 67(2004), no. 1-2, 132–139.Google Scholar
[9] Lester, J., A physical characterization of conformal transformations of Minkowski spacetime. Ann. Discrete Math. 18(1983), 567–574.Google Scholar
[10] Lim, M. H., Rank and tensor rank preservers. In: A survey of linear preserver problems. Linear and Multilinear Algebra 33(1992), no. 1-2, 7–21.Google Scholar
[11] Popovici, I. and D. C. Rˇadulescu, Characterizing the conformality in a Minkowski space. Ann. Inst. H. Poincaré. Sect. A 35(1981), no. 2, 131–148.Google Scholar
[12] Wan, Z.-X., Geometry of Matrices. World Scientific Publishing, River Edge, NJ, 1996.Google Scholar